
已知△ABC∽△A1B1C1,△ABC的周长与△A1B1C1的周长的比值是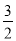 ,BE、B1E1分别是它 们对应边上的中线,且BE=6,则B1E1= .
,BE、B1E1分别是它 们对应边上的中线,且BE=6,则B1E1= .
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:单选题
若 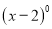 有意义,则
有意义,则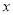 的取值范围是( )
的取值范围是( )
A. 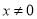 B.
B. 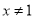 C.
C. 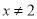 D.
D. 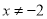
查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:填空题
如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD.若AC=2,则cosD=________.
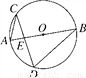
查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:解答题
如图,已知G、H分别是□ABCD对边AD、BC上的点,直线GH分别交BA和DC的延长线于点E、F.
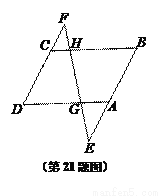
(1)当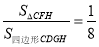 时,求
时,求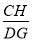 的值;
的值;
(2)联结BD交EF于点M,求证:MG·ME=MF·MH.
(1);(2)详见解析. 【解析】试题分析:(1)由,得.由于△CFH∽△DFG,由相似三角形面积的比等于相似比的平方,即可求得结果; (2)根据平行四边形的性质得出AB∥CD,AD//BC,由平行线分线段成比例得出比例式,即可得出答案. 试题解析:(1)∵, ∴. ∵ □ABCD中,AD//BC, ∴ △CFH∽△DFG , ∴ ()2, ∴=. ...查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:填空题
如图,已知直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3,AB=4,AC=6,DF=9,则DE= .

查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:单选题
已知非零向量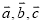 ,下列条件中,不能判定向量
,下列条件中,不能判定向量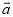 与向量
与向量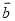 平行的是
平行的是
A. 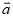 ∥
∥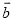
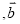 ∥
∥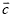 B.
B. 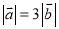 C.
C. 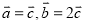 D.
D. 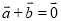
查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:解答题
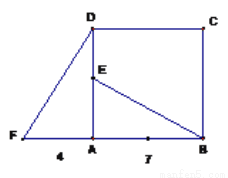
四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7.
(1)旋转中心是点 ,旋转了 度,DE的长度是 ;
(2)BE与DF的关系如何? 请说明理由.(提示:延长BE交DF于点G)
查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:单选题
二次函数y=-3x2-6x+5的图像的顶点坐标是( )
A. (-1,8) B. (1,8) C. (-1,2) D. (1,-4)
A 【解析】试题分析:利用顶点公式,进行解题,,所以顶点坐标是:(-1,8). 故选A.查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年度七年级第一学期人教版数学期末自测试卷(二) 题型:单选题
如图,下面几何体,从左边看得到的平面图形是( )

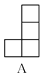
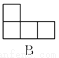
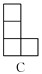
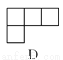
A. A B. B C. C D. D
C 【解析】根据已知条件及左视图的特征即可判断结果. 【解析】 已知条件可知,左视图有2列,每列小正方形数目分别为3,1. 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com