练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    的平方根是______．

    ±2 【解析】∵，而4的平方根是±2， ∴的平方根是±2. 故答案为：±2.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：广东省江门市江海区五校2017-2018学年七年级上学期期末联考数学试卷 题型：单选题

    已知∠A=40°，则∠A的补角等于（　　）

     A、50°  B、90° C、140°  D、180°

    C 【解析】分析：根据补角的和等于180°计算即可． 解答：【解析】 ∵∠A=40°， ∴它的补角=180°-40°=140°． 故答案为：C．

    查看答案和解析>>

    科目：初中数学 来源：2017学年第一学期上海（闵行区）九年级数学质量调研试卷 题型：填空题

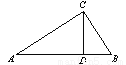
    如图，在Rt△ABC中，∠ACB=90º，CD是高，如果∠A= 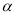，AC = 4，那么BD = ．（用锐角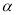的三角比表示）

    4sinαtanα 【解析】试题解析：在中， 在中，根据同角的余角相等可得： 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：陕西省宝鸡市2017-2018学年八年级上学期期中考试数学试卷 题型：解答题

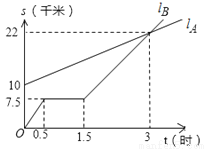
    如图，lA，lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系．

    （1）B出发时与A相距______千米．

    （2）B走了一段路后，自行车发生故障，进行修理，所用的时间是______小时．

    （3）B出发后______小时与A相遇．

    （4）若B的自行车不发生故障，保持出发时的速度前进，______小时与A相遇，相遇点离B的出发点______千米．在图中表示出这个相遇点C．

    （5）求出A行走的路程S与时间t的函数关系式。

    (1)10；（2）1；（3）3；（4）， ；（5）S=4t+10． 【解析】试题分析： （1）由图可知，B出发时与A相距10km； （2）由图可知，B修自行车所用时间为：1.5-0.5=1（小时）； （3）由图象可知，B在出发后3小时的时候与A相遇； （4）分别求出的函数关系式和在修车前的函数关系式，由两个解析式组成方程组，解方程组，即可求得所求答案. 试题解析...

    查看答案和解析>>

    科目：初中数学 来源：陕西省宝鸡市2017-2018学年八年级上学期期中考试数学试卷 题型：填空题

    已知点A（2，1），线段AB∥x轴，且AB=3，则点B的坐标为 ______ ．

    （-1，1）或（5，1）． 【解析】由题意可知点B的纵坐标为1，设点B的横坐标为， ∵点A的坐标为（2，1），线段AB∥x轴，且AB=3， ∴，即或， 解得： 或， ∴点B的坐标为（-1，1）或（5，1）.

    查看答案和解析>>

    科目：初中数学 来源：陕西省宝鸡市2017-2018学年八年级上学期期中考试数学试卷 题型：单选题

    若点A（x，3）与点B（2，y）关于x轴对称，则（　　）

    A. x=-2，y=-3 B. x=2，y=3 C. x=-2，y=3 D. x=2，y=-3

    D 【解析】试题分析：根据平面直角坐标系中对称点的规律可知，若点A（x，3）与点B（2，y）关于x轴对称，则， ．故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017学年度第一学期上海（杨浦区）期末考试初三数学试卷 题型：解答题

    在平面直角坐标系xOy中，抛物线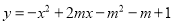交 y轴于点为A，顶点为D，对称轴与x轴交于点H．

    （1）求顶点D的坐标（用含m的代数式表示）；

    （2）当抛物线过点（1，-2），且不经过第一象限时，平移此抛物线到抛物线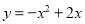的位置，求平移的方向和距离；

    （3）当抛物线顶点D在第二象限时，如果∠ADH=∠AHO，求m的值．

    （1）顶点D（m，1-m）；（2）向左平移了1个单位，向上平移了2个单位；（3）m=－1或m=－2． 【解析】试题分析： 把抛物线的方程配成顶点式，即可求得顶点坐标. 把点代入求出抛物线方程，根据平移规律，即可求解. 分两种情况进行讨论. 试题解析：（1）∵， ∴顶点D（m，1-m）． （2）∵抛物线过点（1，-2）， ∴． 即， ∴或（舍去）...

    查看答案和解析>>

    科目：初中数学 来源：2017学年度第一学期上海（杨浦区）期末考试初三数学试卷 题型：填空题

    抛物线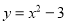的顶点坐标是______．

    （0，-3）. 【解析】试题解析：二次函数， 对称轴 当时， 顶点坐标为： 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：广东省初中部2017-2018学年第一学期期末模拟测试七年级数学试卷 题型：填空题

    将两块直角三角尺的直角顶点重合为如图的位置，若∠AOD=110°，则∠COB=____度．

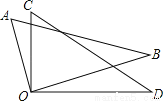
    70 【解析】试题解析：由题意可得∠AOB+∠COD=180°， 又∠AOB+∠COD=∠AOC+2∠COB+∠BOD=∠AOD+∠COB， ∵∠AOD=110°， ∴∠COB=70°．

    查看答案和解析>>

    同步练习册答案