
在平面直角坐标系xOy中,抛物线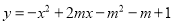 交 y轴于点为A,顶点为D,对称轴与x轴交于点H.
交 y轴于点为A,顶点为D,对称轴与x轴交于点H.
(1)求顶点D的坐标(用含m的代数式表示);
(2)当抛物线过点(1,-2),且不经过第一象限时,平移此抛物线到抛物线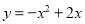 的位置,求平移的方向和距离;
的位置,求平移的方向和距离;
(3)当抛物线顶点D在第二象限时,如果∠ADH=∠AHO,求m的值.
 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源:2017年陕西省西安市中考数学模拟试卷 题型:解答题
阅读下列短文:
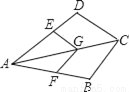
如图,G是四边形ABCD对角线AC上一点,过G作GE∥CD交AD于E,GF∥CB交AB于F,若EG=FG,则有BC=CD成立,同时可知四边形ABCD与四边形AFGE相似.
解答问题:
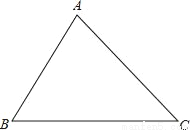
(1)有一块三角形空地(如图△ABC),BC邻近公路,现需在此空地上修建一个正方形广场,其余地为草坪,要使广场一边靠公路,且其面积最大,如何设计,请你在下面图中画出此广场正方形.(尺规作图,不写作法)
(2)锐角△ABC是一块三角形余料,边AB=130mm,BC=150mm,AC=140mm,要把它加工成正方形零件,使正方形的一边在三角形的一边上,其余两个顶点分别在另外两条边上,且剪去正方形零件后剩下的边角料较少,这个正方形零件的边长是多少?你能得出什么结论,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2017学年第一学期上海(闵行区)九年级数学质量调研试卷 题型:单选题
已知抛物线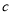 :
: 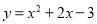 ,将抛物线
,将抛物线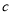 平移得到抛物线
平移得到抛物线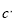 ,如果两条抛物线,关于直线
,如果两条抛物线,关于直线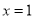 对称,那么下列说法正确的是
对称,那么下列说法正确的是
A. 将抛物线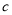 沿
沿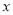 轴向右平移
轴向右平移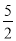 个单位得到抛物线
个单位得到抛物线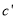 ;
;
B. 将抛物线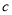 沿
沿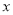 轴向右平移
轴向右平移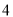 个单位得到抛物线
个单位得到抛物线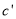 ;
;
C. 将抛物线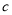 沿
沿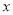 轴向右平移
轴向右平移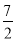 个单位得到抛物线
个单位得到抛物线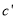 ;
;
D. 将抛物线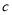 沿
沿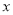 轴向右平移
轴向右平移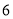 个单位得到抛物线
个单位得到抛物线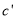 .
.
查看答案和解析>>
科目:初中数学 来源:陕西省宝鸡市2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
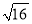 的平方根是______.
的平方根是______.
查看答案和解析>>
科目:初中数学 来源:陕西省宝鸡市2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
下列运算正确的是( )
A. 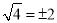 B.
B. 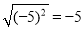 C.
C. 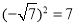 D.
D. 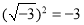
查看答案和解析>>
科目:初中数学 来源:2017学年度第一学期上海(杨浦区)期末考试初三数学试卷 题型:填空题
如图,在□ABCD中,AC、BD相交于点O,点E是OA的中点,联结BE并延长交AD于点F,如果△AEF的面积是4,那么△BCE的面积是_______.
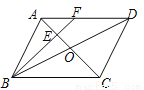
查看答案和解析>>
科目:初中数学 来源:内蒙古赤峰市宁城县2018届九年级上学期期末数学试卷 题型:解答题
如图,两个以点O为圆心的同心圆,
(1)如图1,大圆的弦AB交小圆于C,D两点,试判断AC与BD的数量关系,并说明理由.
(2)如图2,将大圆的弦AB向下平移使其为小圆的切线,切点为C,证明:AC=BC.
(3)在(2)的基础上,已知AB=20cm,直接写出圆环的面积.
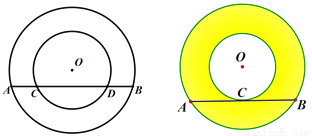
图1 图2
(1)AC=BD;(2)见解析;(3)100πcm2 【解析】试题分析:作OH⊥AB于H,根据垂径定理得到AH=BH,CH=DH,然后利用等量减等量差相等可得到结论. (2) 根据切线的性质以及垂径定理即可证明; (3)根据圆环的面积等于两圆的面积差,再根据切线的性质定理、勾股定理、垂径定理求解. 试题解析:(1)AC=BD,理由是: 过O作OH⊥AB,由垂径定理得A...查看答案和解析>>
科目:初中数学 来源:广东省初中部2017-2018学年第一学期期末模拟测试七年级数学试卷 题型:单选题
深圳是一个美丽的海滨城市,海岸线长约230000米,东临大亚湾,西濒珠江口,数据230000用科学记数法表示为( )
A. 23×104 B. 2.3×105 C. 2.3×106 D. 0.23×107
B 【解析】. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com