
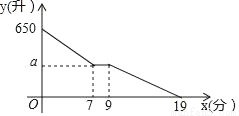
某公司一辆绿化洒水车以每分50升的速度给一片树林浇水,一段时间后关闭洒水阀门,行驶到一片草坪处,以另一洒水速度匀速给草坪浇水,直到洒水车内的水全部用光,洒水车内的水量y(升)与时间x(分)之间的函数图象如图所示.
(1)求a的值;
(2)求洒水车给草坪浇水时y与x之间的函数关系式.
(3)当x=13时,洒水车共浇水多少升?
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(2) 题型:解答题
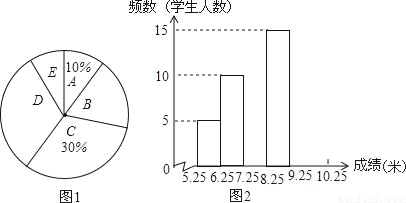
将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.
(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
查看答案和解析>>
科目:初中数学 来源:2017年吉林省中考数学一诊试卷 题型:单选题
﹣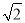 的绝对值是( )
的绝对值是( )
A. ﹣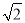 B.
B. 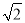 C.
C. 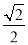 D﹣
D﹣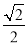
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
反比例函数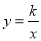 (k≠0)的图象在第一象限内的一支如图所示,P是该图象上一点,A是x轴上一点,PO=PA,S△POA=4,则k的值是( )
(k≠0)的图象在第一象限内的一支如图所示,P是该图象上一点,A是x轴上一点,PO=PA,S△POA=4,则k的值是( )
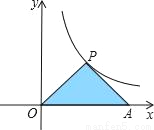
A. 8 B. 4 C. 2 D. 16
B 【解析】根据反比例函数的性质和系数k的几何意义,可知过P作垂线,垂足为B,则三角形POB的面积为,然后根据等腰三角形的性质可知=S△POA=2,解得k=±4,然后根据反比例函数的图像在第一象限,可知k=4. 故选:B.查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是
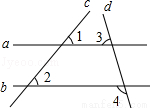
A.35° B.70° C.90° D.110°
D查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:解答题
我校为了创建书香校园,去年购进一批图书,经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.求文学和科普书的单价.
文学书的单价为8元,科普书的单价为12元. 【解析】试题分析:首先设文学书的单价为x元,则科普书的单价为(x+4)元,根据题意可得等量关系:12000元购进的科普书是数量=用8000元购进的文学书本数,根据等量关系列出方程,再解即可. 试题解析:设文学书的单价为x元。 根据题意,得 解得x=8. 经检验,x=8是原方程的解,且符合题意, 8+4=12 答:...查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:填空题
计算:(3a)2=_____.
9a2 【解析】(3a)2=32×a2=9a2, 故答案为:9a2查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:填空题
如图:某同学用一个有60°角的直角三角板估测学校旗杆AB的高度,他将60°角的直角边水平放在1.5米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为5米,则旗杆AB的高度约为__________米。
10.2米 【解析】在△ACE中,CE⊥AE,tan∠ACE=,由此可以求出AE.再根据AB=AE+BE=AE+CD即可求解. 【解析】 由题意可知, 在△ACE中,CE⊥AE,且∠ACE=60°,BD=5, 而tan∠ACE=, ∴AE=CE×tan60°=5. 又∵EB=1.5, ∴AB=AE+EB=AE+CD=+1.5≈10.2(米).查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:解答题
已知A、B、C三点不在同一直线上.
(1)若点A、B、C均在半径为R的⊙O上,
①如图①,当∠A=135°,R=1时,求∠BOC的度数和BC的长.
②如图②,当∠A为锐角时,求证: 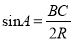 ;
;
(2)若定长线段BC的两个端点分别在∠MAN的两边AM、AN(B、C均与A不重合)滑动,如图③,当∠MAN=60°,BC=2时,分别作BP⊥AM,CP⊥AN,交点为P,试探索在整个滑动过程中,P、A两点间的距离是否保持不变?请说明理由.
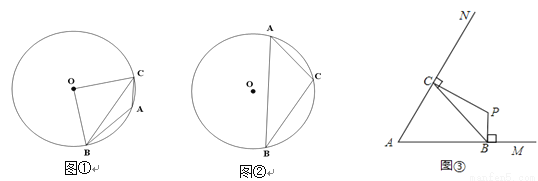
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com