
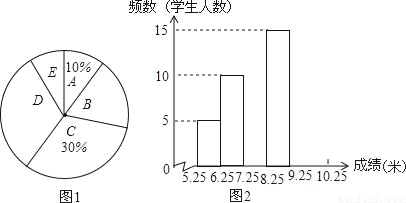
将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.
(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:填空题
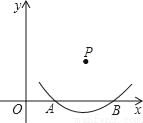
如图,在直角坐标系中,以点P为圆心的圆弧与x轴交于A、B两点,已知P(4,2)和A(2,0),则点B的坐标是_____.
查看答案和解析>>
科目:初中数学 来源:福建省2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
3的相反数是( ).
A. 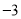 B.
B. 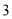 C.
C. 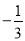 D.
D. 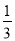
查看答案和解析>>
科目:初中数学 来源:山东省寿光市2017-2018学年七年级上期末模拟数学试卷 题型:单选题
下列各图中,可以是一个正方体的平面展开图的是( )
A. 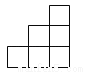 B.
B. 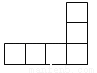 C.
C. 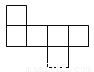 D.
D. 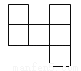
查看答案和解析>>
科目:初中数学 来源:山东省寿光市2017-2018学年七年级上期末模拟数学试卷 题型:单选题
已知x2﹣2x﹣5=0,则2x2﹣4x的值为( )
A. -10 B. 10 C. ﹣2或10 D. 2或﹣10
B 【解析】∵x2﹣2x﹣5=0, ∴x2﹣2x=5, ∴2x2﹣4x=2(x2﹣2x)=2×5=10 即2x2﹣4x的值为10. 故选:B.查看答案和解析>>
科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(2) 题型:填空题
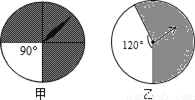
如图,有甲,乙两个可以自由转动的转盘,若同时转动,则停止后指针都落在阴影区域内的概率是_____.
查看答案和解析>>
科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(2) 题型:单选题
等腰三角形一腰上的高与另一腰的夹角为45°,则其顶角为( )
A. 45° B. 135° C. 45°或67.5° D. 45°或135°
D 【解析】①如图,等腰三角形为锐角三角形, ∵BD⊥AC,∠ABD=45°, ∴∠A=45°, 即顶角的度数为45°. ②如图,等腰三角形为钝角三角形, ∵BD⊥AC,∠DBA=45°, ∴∠BAD=45°, ∴∠BAC=135°. 故选:D.查看答案和解析>>
科目:初中数学 来源:2017年吉林省中考数学一诊试卷 题型:填空题
甲、乙两人加工一批零件,甲完成120个与乙完成100个所用的时间相同,已知甲比乙每天多完成4个.设甲每天完成x个零件,依题意列方程 _______.
【解析】设甲每天完成x个零件,依题意列方程: .故答案为: .查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:解答题
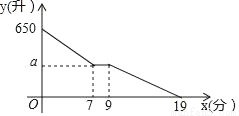
某公司一辆绿化洒水车以每分50升的速度给一片树林浇水,一段时间后关闭洒水阀门,行驶到一片草坪处,以另一洒水速度匀速给草坪浇水,直到洒水车内的水全部用光,洒水车内的水量y(升)与时间x(分)之间的函数图象如图所示.
(1)求a的值;
(2)求洒水车给草坪浇水时y与x之间的函数关系式.
(3)当x=13时,洒水车共浇水多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com