练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，AC平分∠BAD，CM⊥AB于点M，CN⊥AD交AD延长线于点N，若BM＝DN，那么∠ADC与∠ABC的关系是（　　）

    A. 相等 B. 互补

    C. 和为150° D. 和为165°

    B 【解析】∵AC平分∠BAD，CM⊥AB于点M，CN⊥AN， ∴CM=CN，∠CND=∠BMC=90°， ∵BM=DN， 在△CND与△CMB中， ∵ ， ∴△CND≌△CMB， ∴∠B=∠CDN， ∵∠CDN+∠ADC=180°， ∴∠ADC+∠ABC=180°． 故选B．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北京市2017-2018学年第一学期初二数学期中试卷 题型：解答题

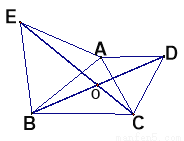
    如图,以△ABC的两边AB、AC向外作等边三角形ABE和等边三角形ACD，连结BD、CE，相交于O.（1）试写出图中和BD相等的一条线段并说明你的理由；（2）求出BD和CE的夹角大小，若改变△ABC的形状，这个夹角的度数会发生变化吗？请说明理由.

    解（1）CE （2），角的大小不变 【解析】（1）找到三角形全等的条件即可 （2）利用（1）中的全等三角形的对应角相等，通过转化角即可

    查看答案和解析>>

    科目：初中数学 来源：云南省2017-2018学年八年级上学期期中考试数学试卷 题型：单选题

    满足下列哪种条件时，能够判定△ABC≌△DEF

    A. AB=DE，BC=EF，∠A=∠E B. AB=DE，BC=EF，∠A=∠D

    C. ∠A=∠E，AB=DF，∠B=∠D D. ∠A=∠D，AB=DE，∠B=∠E

    D 【解析】从选项提供的已知条件开始思考，结合全等三角形的判定方法，与之符合的能够判定全等，不符合的不全等，本题中，D符合ASA，能确定△ABC≌△DEF，其它则不能确定△ABC≌△DEF． 【解析】 A、AB=DE，BC=EF，∠A=∠E，符合SSA，不能判断三角形全等； B、AB=DE，BC=EF，∠C=∠E，符合SSA，不能判断三角形全等； C、∠A=∠E，AB=E...

    查看答案和解析>>

    科目：初中数学 来源：四川省江县初中2016年秋季八年级期末考试试卷 题型：填空题

    计算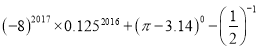： 的结果为_________．

    －9． 【解析】原式==-8×1+1-2=-8+1-2=-9.

    查看答案和解析>>

    科目：初中数学 来源：四川省江县初中2016年秋季八年级期末考试试卷 题型：单选题

    一定能将三角形的面积分成相等的两部分的是三角形的（　　）

    A. 高线 B. 中线 C. 角平分线 D. 都不是

    B 【解析】根据等底同高的两个三角形的面积相等即可知三角形的中线把三角形分成面积相等的两部分．故选B．

    查看答案和解析>>

    科目：初中数学 来源：北京市2017-2018学年第一学期初二数学期中试卷 题型：解答题

    观察下列等式：

    第一个等式：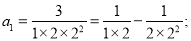

    第二个等式：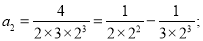

    第三个等式：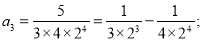

    第四个等式：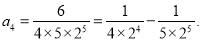

    则式子__________________；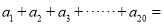

    用含n的代数式表示第n个等式： ____________________________；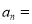

    【解析】试题分析：（1）把这20个数相加，化为左边的形式相加，正好抵消，剩下第一个数分裂的第一项和最后一个数分裂的后一项，得出答案即可； （2）由前四个等是可以看出：是第几个算式，等号左边的分母的第一个因数是就是几，第二个因数是几加1，第三个因数是2的几加1次方，分子是几加2；等号右边分成分子都是1的两项差，第一个分母是几乘2的几次方，第二个分母是几加1乘2的几加1次方；由此规律解决问题. ...

    查看答案和解析>>

    科目：初中数学 来源：北京市2017-2018学年第一学期初二数学期中试卷 题型：解答题

    计算:(1)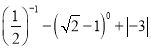

    (2)

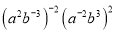
    （3）

    （4）

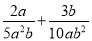
    4, , , x-1 【解析】试题分析：（1）利用负整数指数幂即零指数幂ID运算性质计算即可； （2）直接利用积的乘方运算法则化简，进而利用整式除法运算法则求出答案； （3）首先化简分式，进而通分进行加减运算即可； （4）先算括号里的减法，再把除法化乘法，约分即可. 试题解析：（1）原式=2-1+3=4； （2）原式===； （3）原式===； （4...

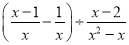
    查看答案和解析>>

    科目：初中数学 来源：北京市2017-2018学年第一学期初二数学期中试卷 题型：单选题

    如图，已知△ABC，则甲、乙、丙三个三角形中和△ABC全等的是（ ）

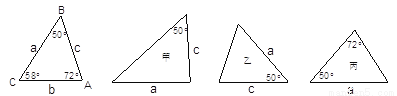
    A. 只有乙 B. 甲和乙 C. 只有丙 D. 乙和丙

    D 【解析】在△ABC和乙三角形中,有两边a、c分别对应相等,且这两边的夹角都为50?，由SAS可知这两个三角形全等； 在△ABC和丙三角形中，有一边a对应相等，和两组角对应相等，由AAS可知这两个三角形全等， 所以在甲、乙、丙三个三角形中和△ABC全等的是乙和丙， 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：安徽省六安市2018届九年级上学期第二次月考数学试卷 题型：填空题

    如图，在平面直角坐标系中，已知点A(2，0)，B(2－a，0)，C(2＋a，0) (a>0)，点P在以D(5，4)为圆心，半径为1的圆上运动，且始终满足∠BPC＝90°，则a的最大值是________

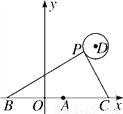
    6 【解析】根据题意，可由AB=2-（2-a）=a=AC，且∠BPC=90°，可知点P位于以点A为圆心，BC为直径的圆上，其直径为2a，此时点P为⊙D和⊙A的交点，当⊙D和⊙A内切时，a有最大值，则⊙A的半径为，其中由A、D点的坐标，可根据勾股定理可知AD=5，所以=5+1=6，即a=6. 故答案为：6.

    查看答案和解析>>

    同步练习册答案