
一定能将三角形的面积分成相等的两部分的是三角形的( )
A. 高线 B. 中线 C. 角平分线 D. 都不是
B 【解析】根据等底同高的两个三角形的面积相等即可知三角形的中线把三角形分成面积相等的两部分.故选B. 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:单选题
如图,在Rt△ABC中,∠ACB=90°,BC=12,AC=5,分别以点A,B为圆心,大于线段AB长度的一半为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连接CD,则△ACD的周长为( )
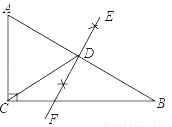
A. 13 B. 17 C. 18 D. 25
C 【解析】在Rt△ABC中,∠ACB=90°,BC=12,AC=5,根据勾股定理求得AB=13.根据题意可知,EF为线段AB的垂直平分线,在Rt△ABC中,根据直角三角形斜边的中线等于斜边的一半可得CD=AD=AB,所以△ACD的周长为AC+CD+AD=AC+AB=5+13=18.故选C.查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
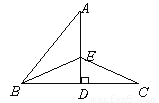
如图, 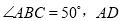 垂直平分线段
垂直平分线段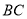 于点
于点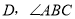 的平分线BE交AD于点
的平分线BE交AD于点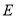 ,连结
,连结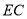 ,则∠C=________
,则∠C=________
查看答案和解析>>
科目:初中数学 来源:四川省江县初中2016年秋季八年级期末考试试卷 题型:填空题
如图,在四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别取一点M,N,使△AMN的周长最小,则∠AMN+∠ANM的度数为____________

查看答案和解析>>
科目:初中数学 来源:四川省江县初中2016年秋季八年级期末考试试卷 题型:填空题
将数0.000000015用科学记数法表示为_____.
1.5×10﹣8 【解析】0.000000015用科学记数法表示为:0.000000015=1.5×10-8.查看答案和解析>>
科目:初中数学 来源:四川省江县初中2016年秋季八年级期末考试试卷 题型:单选题
如图,AC平分∠BAD,CM⊥AB于点M,CN⊥AD交AD延长线于点N,若BM=DN,那么∠ADC与∠ABC的关系是( )

A. 相等 B. 互补
C. 和为150° D. 和为165°
B 【解析】∵AC平分∠BAD,CM⊥AB于点M,CN⊥AN, ∴CM=CN,∠CND=∠BMC=90°, ∵BM=DN, 在△CND与△CMB中, ∵ , ∴△CND≌△CMB, ∴∠B=∠CDN, ∵∠CDN+∠ADC=180°, ∴∠ADC+∠ABC=180°. 故选B.查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题
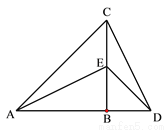
已知如图,将一大、一小两个等腰直角三角尺ABC与DBE拼接(A、B、D三点共线,AB=CB,EB=DB,∠ABC =∠EBD=90°),连接AE、CD.问:AE与CD的位置关系和数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:单选题
已知三角形的两边长分别为3和7,则第三边的中线长x的取值范围是( )
A. 2<x<5 B. 4<x<10 C. 3<x<7 D. 无法确定
A 【解析】如图所示,AB=3,AC=7,延长AD至E,使AD=DE,连接BE、EC, 设AD=x, 在△BDE与△CDA中,, ∴△BDE≌△CDA(SAS), ∴BE=AC=7,AE=2x, 在△ABE中,BE?AB查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:解答题
如图,已知一次函数y=kx+b与反比例函数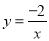 的图象交于A(﹣1,m)、B(n,﹣1)两点.
的图象交于A(﹣1,m)、B(n,﹣1)两点.
(1)求出A、B两点的坐标;
(2)求出这个一次函数的表达式;
(3)根据图象,写出使一次函数值大于反比例函数值的x的范围.
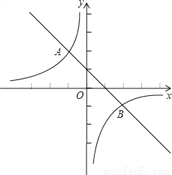
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com