
若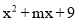 是一个完全平方式,则m=_____.
是一个完全平方式,则m=_____.
科目:初中数学 来源:重庆市江北区2018届九年级上期末模拟数学试卷 题型:单选题
二次根式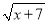 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
A. x≤﹣7 B. x≥﹣7 C. x<﹣7 D. x>﹣7
B 【解析】【解析】 由题意,得:x+7≥0,解得x≥﹣7,故选B.查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市资兴市兴华实验学校中考数学模拟试卷 题型:解答题
解不等式组:  ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:解答题
如图①,在等边三角形ABC中.D是AB边上的动点,以CD为一边,向上作等边三角形EDC.连接AE.
(l)求证:△DBC≌△EAC
(2)试说明AE∥BC的理由.
(3)如图②,当图①中动点D运动到边BA的延长线上时,所作仍为等边三角形,猜想是否仍有AE∥BC?若成立请证明.
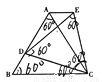
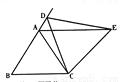
查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:解答题
计算:(1) 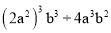 ;
;
(2) 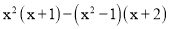 .
.
查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:单选题
如图,在△ABC中,AB=AC,∠A=120 ,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
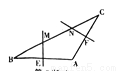
A. 1.5cm B. 2cm C. 2.5cm D. 3cm
B 【解析】连接AM、AN, ∵在△ABC中,AB=AC,∠A=120°,BC=6cm, ∴∠B=∠C=30°, ∵EM垂直平分AB,NF垂直平分AC, ∴BM=AM,CN=AN, ∴∠MAB=∠B=30°,∠NAC=∠C=30°, ∴∠AMN=∠B+∠MAB=60°,∠ANM=∠C+∠NAC=60°, ∴△AMN是等边三角形, ∴AM=MN=...查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:单选题
下列计算正确的是( )
A. 2a+3b=5ab B. 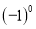 =l C.
=l C. 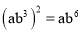 D.
D. 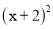
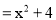
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:填空题
在今年“全国助残日”捐款活动中,某班级第一小组7名同学积极捐出自己的零花钱,奉献自己的爱心.他们捐款的数额分别是(单位:元)50,20,50,30,25,55,25,这组数据的众数_____.
50和25 【解析】【解析】 50、25出现了2次,出现的次数最多,则众数是50和25,故答案为:50和25.查看答案和解析>>
科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:解答题
如图1,已知平行四边形ABCD顶点A的坐标为(2,6),点B在y轴上,且AD∥BC∥x轴,过B,C,D三点的抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,2),点F(m,6)是线段AD上一动点,直线OF交BC于点E.
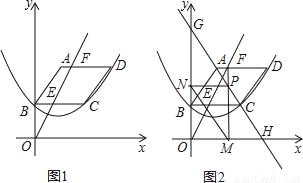
(1)求抛物线的表达式;
(2)设四边形ABEF的面积为S,请求出S与m的函数关系式,并写出自变量m的取值范围;
(3)如图2,过点F作FM⊥x轴,垂足为M,交直线AC于P,过点P作PN⊥y轴,垂足为N,连接MN,直线AC分别交x轴,y轴于点H,G,试求线段MN的最小值,并直接写出此时m的值.
(1)抛物线解析式为y=x2﹣x+3;(2)S=m﹣3(2<m≤6);(3)当m=时,MN最小=. 【解析】试题分析:(1)根据平行四边形的性质和抛物线的特点确定出点D,然而用待定系数法确定出抛物线的解析式.(2)根据AD∥BC∥x轴,且AD,BC间的距离为3,BC,x轴的距离也为3,F(m,6),确定出E(,3),从而求出梯形的面积.(3)先求出直线AC解析式,然后根据FM⊥x轴,表示出点...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com