练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

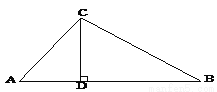
    如图，在Rt△ABC中∠ACB=90°，CD⊥AB于D ．已知AC=6,AD=2求AB？

    18． 【解析】 试题分析：利用△ACD∽△ABC得：AD:AC=AC:AB可求AB的值． 试题解析：∵CD⊥AB ∴∠ADC=90° ∴∠A+∠ACD=90° 又∠A+∠B=90° ∴∠ACD=∠B ∴△ACD∽△ABC ∴AD:AC=AC:AB ∴AB=18．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年黑龙江省大庆市中考数学三模试卷 题型：解答题

    计算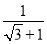： ﹣sin60°+ ．

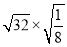    . 【解析】试题分析：根据特殊角的三角函数、二次根式的化简进行计算即可． 试题解析：原式=﹣+4×=﹣+2=+2=．

    查看答案和解析>>

    科目：初中数学 来源：吉林省吉林市2016-2017年七年级上期期末数学试卷 题型：解答题

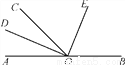
    如图，O为直线AB上一点，∠AOC＝50°，OD平分∠AOC，∠DOE＝90°.

    (1)请你数一数，图中有多少个小于平角的角；

    (2)求出∠BOD的度数；

    (3)请通过计算说明OE是否平分∠BOC.

    （1）9；（2）155°；（3）OE平分∠BOC.理由见解析. 【解析】试题分析：（1）小于平角的角即小于∠AOB的角，可以从OA为边，顺时针数，注意做到不重不漏； （2）可根据角平分线的定义和平角的定义求解； （3）分别求出∠COE，∠BOE的值，再做判断． 【解析】 （1）图中有9个小于平角的角； （2）因为OD平分∠AOC，∠AOC=50° 所以∠AOD...

    查看答案和解析>>

    科目：初中数学 来源：吉林省吉林市2016-2017年七年级上期期末数学试卷 题型：单选题

    下列说法中错误的是( )

    A. 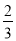－x2y的系数是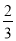－ B. 0是单项式

    C. 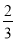xy的次数是1 D. －x是一次单项式

    C 【解析】A选项中，因为的系数是，所以本选项正确； B选项中，因为0是单项式， 所以本选项正确； C选项中，因为的次数是2，不是1，所以本选项错误； D选项中，因为是一次单项式，所以本选项正确； 故选C.

    查看答案和解析>>

    科目：初中数学 来源：吉林省吉林市2016-2017年七年级上期期末数学试卷 题型：单选题

    －6的倒数是( )

    A. 6 B. －6 C. 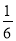D. －

    D 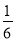【解析】分析：根据两个数乘积是1的数互为倒数的定义，因此求一个数的倒数即用1除以这个数．所以的倒数为。故选D。

    查看答案和解析>>

    科目：初中数学 来源：吉林省长春市区2018届九年级上期末模拟数学试卷（解析版） 题型：填空题

    如图，△ABC与△DEF是位似图形，位似比为2：3，则△ABC与△DEF的面积比为 ________

    4：9 【解析】试题解析：∵△ABC与△DEF是关于点O的位似图形，△ABC与△DEF的位似比为：2:3， ∴△ABC与△DEF的相似比为：2:3， ∴△ABC与△DEF的面积比为：4:9. 故答案为：4:9.

    查看答案和解析>>

    科目：初中数学 来源：吉林省长春市区2018届九年级上期末模拟数学试卷（解析版） 题型：单选题

    设计师以y=2x2﹣4x+8的图形为灵感设计杯子如图所示，若AB=4，DE=3，则杯子的高CE=（　　）

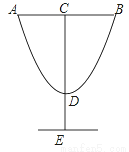
    A. 17                           B. 11                            C. 8 D. 7

    B 【解析】试题解析： ∴D(1,6)， ∵AB=4， ∴AC=BC=2， ∴点A的横坐标为?1， 当x=?1时, ∴CD=14?6=8， ∴CE=DE+CD=3+8=11， 则杯子的高CE为11. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版七年级数学下册（广西）期末测试 题型：填空题

    某超市账目记录显示，第一天卖出39支牙刷和21盒牙膏，收入396元；第二天以同样的价格卖出同样的52支牙刷和28盒牙膏，收入应该是____________元.

    528 【解析】试题解析：设一支牙刷收入x元，一盒牙膏收入y元，由题意，得 39x+21y=396， ∴13x+7y=132， ∴52x+28y=528.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷（B卷） 题型：解答题

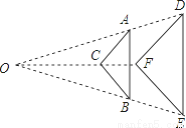
    如图，四边形ABCD中AC平分∠BAD，∠ADC=∠ACB=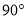，E为AB的中点，AC与DE交于点F．

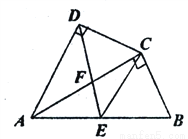
    (1)求证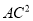： =AB·AD；

    (2)求证：CE//AD；

    (3)若AD=6， AB=8．求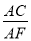的值．

    (1)证明见解析； (2)证明见解析； (3) ． 【解析】试题分析：（1）由AC平分∠BAD，∠ADC=∠ACB=90°，可证得△ADC∽△ACB，然后由相似三角形的对应边成比例，证得AC2=AB•AD； （2）由E为AB的中点，根据在直角三角形中，斜边上的中线等于斜边的一半，即可证得CE=AB=AE，继而可证得∠DAC=∠ECA，得到CE∥AD； （3）易证得△AFD∽△CF...

    查看答案和解析>>

    同步练习册答案