
设计师以y=2x2﹣4x+8的图形为灵感设计杯子如图所示,若AB=4,DE=3,则杯子的高CE=( )
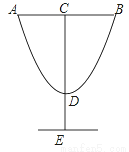
A. 17 B. 11 C. 8 D. 7
B 【解析】试题解析: ∴D(1,6), ∵AB=4, ∴AC=BC=2, ∴点A的横坐标为?1, 当x=?1时, ∴CD=14?6=8, ∴CE=DE+CD=3+8=11, 则杯子的高CE为11. 故选B.科目:初中数学 来源:2017年黑龙江省大庆市中考数学三模试卷 题型:单选题
将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )
A. 360° B. 540° C. 720° D. 900°
D 【解析】根据题意列出可能情况,再分别根据多边形的内角和定理进行解答即可. 【解析】 ①将矩形沿对角线剪开,得到两个三角形,两个多边形的内角和:180°+180°=360°; ②将矩形从一顶点剪向对边,得到一个三角形和一个四边形,两个多边形的内角和为:180°+360°=540°; ③将矩形沿一组对边剪开,得到两个四边形,两个多边形的内角和为:180°+540°=720...查看答案和解析>>
科目:初中数学 来源:吉林省吉林市2016-2017年七年级上期期末数学试卷 题型:单选题
钟表在8:25时,时针与分针的夹角度数是( )
A. 101.5 B. 102.5 C. 120 D. 125
B 【解析】 ,故选B.查看答案和解析>>
科目:初中数学 来源:吉林省长春市区2018届九年级上期末模拟数学试卷(解析版) 题型:解答题
如图,在Rt△ABC中∠ACB=90°,CD⊥AB于D .已知AC=6,AD=2求AB?
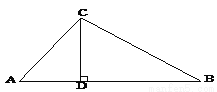
查看答案和解析>>
科目:初中数学 来源:吉林省长春市区2018届九年级上期末模拟数学试卷(解析版) 题型:填空题
若y=xm﹣2是二次函数,则m= .
4. 【解析】 试题分析:∵函数y=xm﹣2是二次函数,∴m﹣2=2,∴m=4. 故答案为4.查看答案和解析>>
科目:初中数学 来源:吉林省长春市区2018届九年级上期末模拟数学试卷(解析版) 题型:单选题
如图,已知DE∥FG∥BC,且将△ABC分成面积相等的三部分,若BC=15,则FG的长度是( )
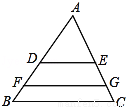
A. 5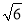 B. 10 C. 4
B. 10 C. 4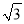 D. 7.5
D. 7.5
查看答案和解析>>
科目:初中数学 来源:2018年春人教版七年级数学下册(广西)期末测试 题型:解答题
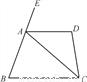
如图,在四边形ABCD中,∠D=100°,CA平分∠BCD,∠ACB=40°,∠BAC=70°,延长BA至点E.
(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
查看答案和解析>>
科目:初中数学 来源:2018年春人教版七年级数学下册(广西)期末测试 题型:单选题
下列说法不正确的是( )
A. 4是16的算术平方根 B. 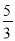 是
是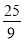 的一个平方根
的一个平方根
C. (-6)2的平方根-6 D. (-3)3的立方根-3
C 【解析】试题分析:A、因为42=16,所以4是16的算术平方根,正确; B、因为,所以的平方根是±,所以是的一个平方根,正确; C、(-6)2=36,36的平方根是±6,此项错误; D、(-3)3的立方根-3正确. 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(B卷) 题型:填空题
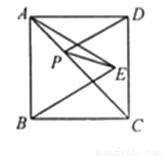
如图,正方形ABCD的面积为25, 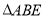 为等边三角形,点E在正方形ABCD内,若P是对角线AC上的一动点,则
为等边三角形,点E在正方形ABCD内,若P是对角线AC上的一动点,则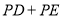 的最小值是__________.
的最小值是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com