
计算: 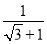 ﹣sin60°+
﹣sin60°+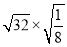 .
.
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源:2017年湖北省随州市中考数学模拟试卷 题型:解答题
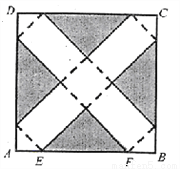
如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于底面上一点).已知E、F在AB边上,是被剪去一个等腰直角三角形斜边的两个端点,设AE=BF=xcm.
(1)若折成的包装盒恰好是正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
查看答案和解析>>
科目:初中数学 来源:2017年湖北省随州市中考数学模拟试卷 题型:单选题
贯彻落实“大气十条”,抓好大气污染防治,是今年环保工作的重中之重.其中推进燃煤电厂脱硫改造15000 000千瓦是《政府工作报告》中确定的重点任务之一.将数据15 000 000用科学记数法表示为( )
A. 15×106 B. 1.5×107 C. 1.5×108 D. 0.15×108
B 【解析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.即15 000 000=1.5×107.故选B.查看答案和解析>>
科目:初中数学 来源:2017年黑龙江省大庆市中考数学三模试卷 题型:解答题
学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、“羽毛球”、“乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图.
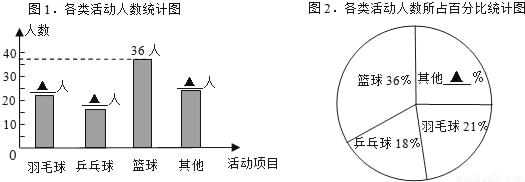
(1)学校采用的调查方式是 ;学校共选取了 名学生;
(2)补全统计图中的数据:条形统计图中羽毛球 人、乒乓球 人、其他 人、扇形统计图中其他 %;
(3)该校共有1200名学生,请估计喜欢“乒乓球”的学生人数.
(1)抽样调查,100;(2)21,18,25,25%;(3)估计喜欢“乒乓球”的学生人数有180人. 【解析】试题分析:(1)属于抽样调查.根据所占人数÷总人数×100%=百分比,计算即可; (2)根据百分比公式计算即可; (3)用样本估计总体的思想解决问题; 试题解析:(1)学校采用的调查方式是抽样调查, 总人数=36÷36%=100(名), 故答案为:抽样...查看答案和解析>>
科目:初中数学 来源:2017年黑龙江省大庆市中考数学三模试卷 题型:填空题
对于任意实数m、n,定义一种运算m※n=mn﹣m﹣n+3,等式的右边是通常的加减和乘法运算,例如:3※5=3×5﹣3﹣5+3=10.请根据上述定义解决问题:若a<2※x<7,且解集中有两个整数解,则a的取值范围是_____.
4≤a<5 【解析】试题分析:根据题意得:2※x=2x﹣2﹣x+3=x+1,∵a<x+1<7,即a﹣1<x<6解集中有两个整数解,∴a的范围为,故答案为: .查看答案和解析>>
科目:初中数学 来源:2017年黑龙江省大庆市中考数学三模试卷 题型:单选题
将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )
A. 360° B. 540° C. 720° D. 900°
D 【解析】根据题意列出可能情况,再分别根据多边形的内角和定理进行解答即可. 【解析】 ①将矩形沿对角线剪开,得到两个三角形,两个多边形的内角和:180°+180°=360°; ②将矩形从一顶点剪向对边,得到一个三角形和一个四边形,两个多边形的内角和为:180°+360°=540°; ③将矩形沿一组对边剪开,得到两个四边形,两个多边形的内角和为:180°+540°=720...查看答案和解析>>
科目:初中数学 来源:2017年湖北省黄冈市中考数学二模试卷 题型:填空题
关于x的分式方程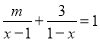 的解为正数,则m的取值范围是_____.
的解为正数,则m的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源:吉林省长春市区2018届九年级上期末模拟数学试卷(解析版) 题型:解答题
如图,在Rt△ABC中∠ACB=90°,CD⊥AB于D .已知AC=6,AD=2求AB?
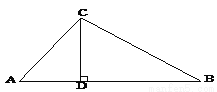
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com