
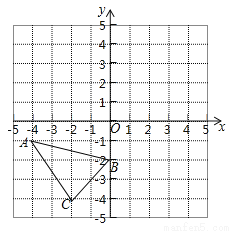
如图,△ABC的三个顶点都在边长为1的小正方形组成的网格的格点上,以点O为原点建立直角坐标系,回答下列问题:
(1)将△ABC先向上平移5个单位,再向右平移1个单位得到△A1B1C1,画出△A1B1C1,并直接写出A1的坐标 ;
(2)将△A1B1C1绕点(0,﹣1)顺时针旋转90°得到△A2B2C2,画出A2B2C2;
(3)观察图形发现,A2B2C2是由△ABC绕点 顺时针旋转 度得到的.
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市七年级数学科期末检测模拟 题型:单选题
如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )
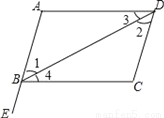
A. ∠1=∠2 B. ∠3=∠4 C. ∠C=∠CBE D. ∠C+∠ABC=180°
B 【解析】A. ∵∠1=∠3,∴AB∥CD, 故不正确; B. ∵ ∠2=∠4 , ∴AD∥BC, 故正确; C. ∵∠C=∠CBE , ∴AB∥CD, 故不正确; D. ∵∠C+∠ABC=180º, ∴AB∥CD, 故不正确; 故选B.查看答案和解析>>
科目:初中数学 来源:山东省德州市2018届九年级上期末模拟数学试卷 题型:解答题
如图,已知抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
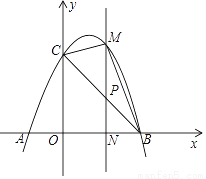
(1)求A,B,C三点的坐标;
(2)若点P为线段BC上一点(不与B,C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求点P的坐标;
(3)在(2)的条件下,当△BCM的面积最大时,在抛物线的对称轴上存在一点Q,使得△CNQ为直角三角形,求点Q的坐标.
(1)C(0,3),A(﹣1,0),B(3,0);(2)当t=时,△BCM的面积最大,此时P点坐标为( , );(3)Q点的坐标为(1, )或(1, )或(1, )或(1,﹣). 【解析】试题分析:(1)在抛物线解析式中,令x=0可求得C点坐标,令y=0则可求得A、B的坐标;(2)由B、C的坐标可求得直线BC的解析式为y=﹣x+3,可设P点坐标为(t,﹣t+3),则可表示出M点坐标,则可求得...查看答案和解析>>
科目:初中数学 来源:山东省德州市2018届九年级上期末模拟数学试卷 题型:单选题
圆锥的底面半径为2,母线长为4,则它的侧面积为( )
A. 8π B. 16π C. 4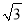 π D. 4π
π D. 4π
查看答案和解析>>
科目:初中数学 来源:山东省德州市2018届九年级上期末模拟数学试卷 题型:单选题
下列方程一定是一元二次方程的是( )
A. x2+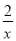 ﹣1=0 B. 2x2﹣y﹣3=0 C. ax2﹣x+2=0 D. 3x2﹣2x﹣1=0
﹣1=0 B. 2x2﹣y﹣3=0 C. ax2﹣x+2=0 D. 3x2﹣2x﹣1=0
查看答案和解析>>
科目:初中数学 来源:山东省德州市2018届九年级上期中数学试卷 题型:填空题
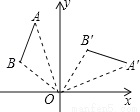
如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是_________________.
查看答案和解析>>
科目:初中数学 来源:山东省德州市2018届九年级上期中数学试卷 题型:单选题
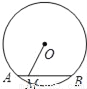
如图,⊙O的半径为5,弦AB的长为8,点M在线段AB(包括端点A,B)上移动,则OM的取值范围是( )
A. 3≤OM≤5 B. 3≤OM<5 C. 4≤OM≤5 D. 4≤OM<5
A 【解析】试题分析:当M与A或B重合时,达到最大值;当OM⊥AB时,为最小. 【解析】 当M与A或B重合时,达到最大值,即圆的半径5; 当OM⊥AB时,为最小值==3. 故OM的取值范围是:3≤OM≤5. 故选A.查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:填空题
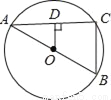
如图,AB是⊙O的直径,OD⊥AC于点D,BC=6cm,则OD=_____cm.
查看答案和解析>>
科目:初中数学 来源:江苏省丹阳市2017-2018学年七年级12月月考数学试卷 题型:填空题
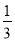 x2y是__次单项式.
x2y是__次单项式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com