
如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线,若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( )
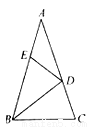
A. 2个 B. 3个 C. 4个 D. 5个
D 【解析】试题分析:在△ABC中,∠A=36°,AB=AC,求得∠ABC=∠C=72°,且△ABC是等腰三角形;因为CD是△ABC的角平分线,所以∠ACD=∠DCB=36°,所以△ACD是等腰三角形;在△BDC中,由三角形的内角和求出∠BDC=72°,所以△BDC是等腰三角形;所以BD=BC=BE,所以△BDE是等腰三角形;所以∠BDE=72°,∠ADE=36°,所以△ADE是等腰三角形.... 习题精选系列答案
习题精选系列答案科目:初中数学 来源:北京四中2017-2018学年上学期初中八年级期中考试数学试卷 题型:单选题
某工程队准备修建一条长1200米的道路,由于采用新的施工方式,实际每天修建道路的速度比原计划快20%,结果提前两天完成任务,若设原计划每天修建道路x米,则根据题意可列方程为( ).
A. 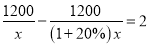 B.
B. 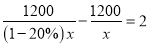
C. 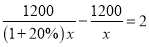 D.
D. 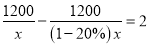
查看答案和解析>>
科目:初中数学 来源:天津市宝坻区口东镇2018届九年级12月月考数学试卷 题型:填空题
在一个不透明的口袋中,装有若干个红球和6个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验发现,摸到黄球的频率是0.3,则估计盒子中大约有红球___________。
14个 【解析】设红球有 x 个,根据题意得, 解得 x=14.所以盒子中大约有红球14个.查看答案和解析>>
科目:初中数学 来源:山东省临沂市费县2017-2018学年八年级(上)期中数学试卷 题型:解答题
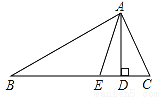
已知:如图,在△ABC中,AD、AE分别是△ABC的高和角平分线.
(1)若∠B=30°,∠C=50°,求∠DAE的度数.
(2)试问∠DAE与∠C﹣∠B有怎样的数量关系?说明理由.
查看答案和解析>>
科目:初中数学 来源:山东省临沂市费县2017-2018学年八年级(上)期中数学试卷 题型:解答题
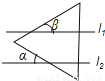
如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于______.
查看答案和解析>>
科目:初中数学 来源:山东省临沂市费县2017-2018学年八年级(上)期中数学试卷 题型:单选题
两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=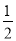 AC;③△ABD≌△CBD,其中正确的结论有( )
AC;③△ABD≌△CBD,其中正确的结论有( )
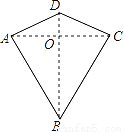
A. 0个 B. 1个 C. 2个 D. 3个
D 【解析】试题解析:在△ABD与△CBD中, , ∴△ABD≌△CBD(SSS), 故③正确; ∴∠ADB=∠CDB, 在△AOD与△COD中, , ∴△AOD≌△COD(SAS), ∴∠AOD=∠COD=90°,AO=OC, ∴AC⊥DB, 故①②③正确; 故选D.查看答案和解析>>
科目:初中数学 来源:重庆市江北区联盟校2018届九年级(上)期中数学试卷 题型:解答题
设a,b是任意两个实数,规定a与b之间的一种运算“⊕”为:a⊕b= ,
,
例如:1⊕(﹣3)=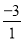 =﹣3,(﹣3)⊕2=(﹣3)﹣2=﹣5,(x2+1)⊕(x﹣1)=
=﹣3,(﹣3)⊕2=(﹣3)﹣2=﹣5,(x2+1)⊕(x﹣1)=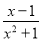 (因为x2+1>0),
(因为x2+1>0),
参照上面材料,解答下列问题:
(1)2⊕4= ,(﹣2)⊕4= ;
(2)若x>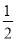 ,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
查看答案和解析>>
科目:初中数学 来源:重庆市江北区联盟校2018届九年级(上)期中数学试卷 题型:单选题
某商品原价200元,连续两次降价a%后售价为148元,下列所列方程正确的是( )
A. 200(1+a%)2=148 B. 200(1﹣a%)2=148 C. 200(1﹣2a%)=148 D. 200(1﹣a2%)=148
B 【解析】试题分析:主要考查增长率问题,本题可用降价后的价格=降价前的价格×(1-降价率),首先用x表示两次降价后的售价,然后由题意可列出方程.依题意得两次降价后的售价为200(1-a%)2,因此可得方程200(1-a%)2=148. 故选B查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:解答题
如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
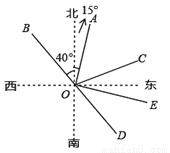
(1)射线OC的方向是___________________;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
(1)北偏东70°;(2)70°;(3)90°. 【解析】 试题分析:(1)先求出∠AOB=55°,再求得∠NOC的度数,即可确定OC的方向;(2)根据∠AOB=55°,∠AOC=∠AOB,得出∠BOC=110°,进而求出∠COD的度数;(3)根据射线OE平分∠COD,即可求出∠COE=35°再利用∠AOC=55°求出答案即可. 试题解析:(1)∵OB的方向是北偏西40°,OA的...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com