练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

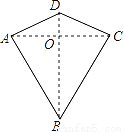
    两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，詹姆斯在探究筝形的性质时，得到如下结论：①AC⊥BD；②AO=CO=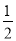AC；③△ABD≌△CBD，其中正确的结论有（　　）

    A. 0个 B. 1个 C. 2个 D. 3个

    D 【解析】试题解析：在△ABD与△CBD中， ， ∴△ABD≌△CBD（SSS）， 故③正确； ∴∠ADB=∠CDB， 在△AOD与△COD中， ， ∴△AOD≌△COD（SAS）， ∴∠AOD=∠COD=90°，AO=OC， ∴AC⊥DB， 故①②③正确； 故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北京四中2017-2018学年上学期初中八年级期中考试数学试卷 题型：单选题

    在平面直角坐标系中，点A，点B关于y轴对称，点A的坐标是（2，-8），则点B的坐标是（ ）.

    A. （-2，-8） B. （2，8） C. （-2，8） D. （8，2）

    A 【解析】试题解析：根据关于轴的对称点的坐标特点：横坐标互为相反数，纵坐标不变. ∵点A,点B关于y轴对称,点A的坐标是(2,?8)， ∴点B的坐标是(?2,?8)， 故选：A.

    查看答案和解析>>

    科目：初中数学 来源：天津市宝坻区口东镇2018届九年级12月月考数学试卷 题型：单选题

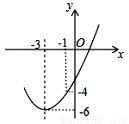
    如图，已知顶点为（－3，－6）的抛物线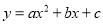经过点（－1，－4），下列结论：①b2＞4ac；②ax2+bx+c≥－6；③若点（－2，m），（－5，n）在抛物线上，则m＞n；④关于x的一元二次方程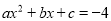的两根为﹣5和﹣1，其中正确的有（ ）

    A. 1个 B. 2个 C. 3个 D. 4个

    C 【解析】∵抛物线与x轴有2个交点，∴△=b2?4ac>0，即b2>4ac，所以①正确； ∵抛物线的顶点坐标为(?3，?6)，即x=?3时，函数有最小值，∴ax2+bx+c??6，所以②正确； ∵抛物线的对称轴为直线x=?3，而点(?2，m)，(?5，n)在抛物线上，∴m

    查看答案和解析>>

    科目：初中数学 来源：山东省临沂市费县2017-2018学年八年级（上）期中数学试卷 题型：填空题

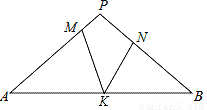
    如图，在△PAB中，PA=PB，M，N，K分别是PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=44°，则∠P的度数为　 　．

    92° 【解析】【解析】 ∵PA=PB，∴∠A=∠B，在△AMK和△BKN中，∵AM=BK，∠A=∠B，AK=BN，∴△AMK≌△BKN，∴∠AKM=∠BNK，∵∠AKN=∠B+∠BNK，即∠AKM+∠MKN=∠B+∠BNK，∴∠B=∠MKN=44°，∴∠P=180°﹣2×44°=92°．故答案为：92°．

    查看答案和解析>>

    科目：初中数学 来源：山东省临沂市费县2017-2018学年八年级（上）期中数学试卷 题型：单选题

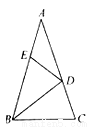
    如图，在△ABC中，∠A=36°，AB=AC，BD是△ABC的角平分线，若在边AB上截取BE=BC，连接DE,则图中等腰三角形共有（ ）

    A. 2个 B. 3个 C. 4个 D. 5个

    D 【解析】试题分析：在△ABC中，∠A=36°，AB=AC，求得∠ABC=∠C=72°，且△ABC是等腰三角形；因为CD是△ABC的角平分线，所以∠ACD=∠DCB=36°，所以△ACD是等腰三角形；在△BDC中，由三角形的内角和求出∠BDC=72°，所以△BDC是等腰三角形；所以BD=BC=BE，所以△BDE是等腰三角形；所以∠BDE=72°，∠ADE=36°，所以△ADE是等腰三角形．...

    查看答案和解析>>

    科目：初中数学 来源：重庆市江北区联盟校2018届九年级（上）期中数学试卷 题型：解答题

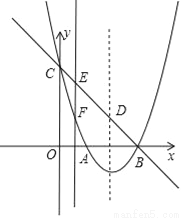
    如图，抛物线y=ax2+bx+c（a≠0）的顶点坐标为（2，﹣1），图象与y轴交于点C（0，3），与x轴交于A、B两点．

    （1）求抛物线的解析式；

    （2）设抛物线对称轴与直线BC交于点D，连接AC、AD，求△ACD的面积；

    （3）点E为直线BC上的任意一点，过点E作x轴的垂线与抛物线交于点F，问是否存在点E使△DEF为直角三角形？若存在，求出点E坐标，若不存在，请说明理由．

    （1）抛物线解析式为y=x2﹣4x+3；（2）S△ACD=2；（3）存在满足条件的点E，其坐标为（2+，1﹣）或（2﹣，1+）或（1，2）或（4，﹣1）． 【解析】试题分析：（1）设顶点式y=a（x-2）2-1（a≠0），然后把C点坐标代入求出a即可； （2）通过解方程x2-4x+3=0得A（1，0），B（3，0），再利用待定系数法求出直线BC解析式为y=-x+3，从而得到D（2，1），然...

    查看答案和解析>>

    科目：初中数学 来源：重庆市江北区联盟校2018届九年级（上）期中数学试卷 题型：解答题

    解方程：（1）x2﹣2x=5 （2）2（x﹣3）=3x（x﹣3）

    （1）；（2）. 【解析】试题分析：（1）根据配方法可以解答此方程； （2）先移项，然后根据提公因式法可以解答此方程． 试题解析：（1）∵x2﹣2x=5， ∴x2﹣2x+1=5+1， ∴（x+1）2=6， ∴ ， 解得： ， ； （2）∵2（x﹣3）=3x（x﹣3）， ∴2（x﹣3）﹣3x（x﹣3）=0， ∴（x﹣3）（2﹣3x）=0， ...

    查看答案和解析>>

    科目：初中数学 来源：重庆市江北区联盟校2018届九年级（上）期中数学试卷 题型：单选题

    4的倒数是（　　）

    A. ﹣4 B. 4 C. ﹣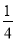 D.

    D 【解析】试题解析：根据乘积是1的两个数互为倒数，可得4的倒数是， 故选D．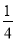

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册 第四章 基本平面图形练习题 题型：单选题

    如图，已知A、B、C、D、E五点在同一直线上，点D是线段AB的中点，点E是线段BC的中点，若线段AC＝12，则线段DE等于（ ）

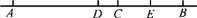
    A. 10 B. 8 C. 6 D. 4

    C 【解析】∵D点是线段AB的中点，∴AD=BD， ∵点E是线段BC的中点，∴BE=CE， ∵AC=12，∴AD+CD=12，∴BD+CD=12， 又∵BD=2CE+CD，∴2CE+CD+CD=12， 即2(CE+CD)=12，∴CE+CD=6， 即线段DE等于6. 故选：C.

    查看答案和解析>>

    同步练习册答案