
һֻ�����Ĵ�����װ��1������1�������1��������Щ�����ɫ�ⶼ��ͬ��
��1�����Ⱥ�Ӵ�������������1��������������ĸ��ʣ�
��2�����Ⱥ�Ӵ�������������1����¼��ɫ��Żء����ȣ��ٴ�����������1���������ζ���������ĸ��ʣ�
��1������2���� �������� �����������1��ֱ�����ø��ʹ�ʽ��⣻ ��2�������û���״ͼչʾ����9�ֵȿ��ܵĽ���������ҳ����ζ���������Ľ������Ȼ����ݸ��ʹ�ʽ��⣮ �����������1����������ĸ���=�� ��2������״ͼΪ�� ����9�ֵȿ��ܵĽ�������������ζ���������Ľ����Ϊ1���������ζ���������ĸ���=�� ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ������������2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
֤��������ƽ��ֱ�߱�������ֱ�����أ�һ��ͬ���ڽǵ�ƽ�����ഹֱ.
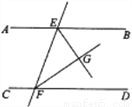
��֪:
��֤�� .
֤����
������. ������������������������⻭��ͼ�Σ�д����֪����֤��֤������Ϊ����AB��CDƽ�У�������ֱ��ƽ��ͬ���ڽǻ����õ���BEF+��EFD=180�㣬����EG��FGΪ��ƽ���ߣ����ý�ƽ���߶��弰���������õ���GEF+��EFG=90�㣬���������ε��ڽǺͶ������ɵá�EGF=90�㣬���۵�֤�� ��������� ��֪��ֱ��AB��CD��ֱ��EF�ֱ�AB��CD�ڵ�E��F����BEF����EFD...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹŶ�����˹��2017-2018ѧ���һѧ�������Ծ���һ��ѧ. ���ͣ���ѡ��
����ֵС��3����������֮���ǣ� ��
A. O B. 3 C. -3 D. 6
A ��������1+2+3+0-1-2-3=0,����ѡA.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�����ϳ���������ѧ2017-2018ѧ����꼶��ѧ���п�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ����
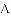
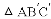 ��λ�ã�ʹ��
��λ�ã�ʹ��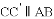 ����
����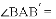 �� ����
�� ����
A. 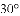
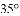
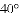
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꽭��ʡ�������п���ѧģ���Ծ� ���ͣ������
��֪������y=x2��2mx+m2+m��1��m�dz������Ķ���ΪP��ֱ��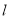 ��y=x��1
��y=x��1
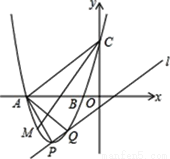
��1����֤����P��ֱ��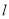 �ϣ�
�ϣ�
��2����m=��3ʱ����������x�ύ��A��B���㣬��y�ύ�ڵ�C����ֱ��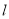 ����һ������ΪQ��M��x���·��������ϵ�һ�㣬��ACM=��PAQ����ͼ�������M�����ꣻ
����һ������ΪQ��M��x���·��������ϵ�һ�㣬��ACM=��PAQ����ͼ�������M�����ꣻ
��3�����������ߺ�ֱ��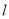 ���������㼰����ԭ��Ϊ������������ǵ��������Σ���ֱ��д�����з���������m��ֵ��
���������㼰����ԭ��Ϊ������������ǵ��������Σ���ֱ��д�����з���������m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꽭��ʡ�������п���ѧģ���Ծ� ���ͣ������
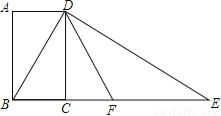
��ͼ���ı���ABCDΪ���Σ�����D���Խ���BD�Ĵ��ߣ���BC���ӳ����ڵ�E��ȡBE���е�F������DF��DF=4����AB=x��AD=y����x2+��y��4��2��ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꽭��ʡ�������п���ѧģ���Ծ� ���ͣ������
�ֽ���ʽ��x2��9=_____��
��x+3����x��3�� ��������x2��9=��x+3����x��3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡͭ����������2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
��ϣ����ѧ�Ұ�1��3��6��10��15��21�������������������������Ĺ��ɣ���100�������������98�����������IJ�Ϊ__________.
199 �����������������ڶ����ȵ�һ����2���������ȵڶ�����3�����ĸ��ȵ�������4���������ƣ����Եõ�����n���ȵ�n-1����n�����100�������������99�����������IJ�100����99�������������98�����������IJ�99�����100�������������98�����������IJ�Ϊ100+99=199���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ��� ���꼶��ѧ��ĩ���Ծ� ���ͣ������
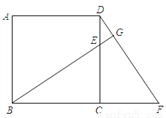
��ͼ�������εı߳�Ϊ4��E��CD��һ�㣬��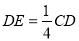 ������BCE�Ƶ�C˳ʱ����ת90��á�DCF.
������BCE�Ƶ�C˳ʱ����ת90��á�DCF.
��1����CF�ij���
��2����DF�ij���
��3���ӳ�BE��DF��G�㣬���ж�ֱ��BG��DF��λ�ù�ϵ����˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com