
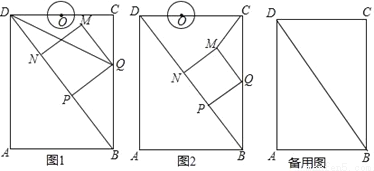
如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上.点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,1cm半径作⊙O.点P与点D同时出发,设它们的运动时间为t(单位:s) (0≤t≤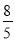 ).
).
(1)如图1,连接DQ,若DQ平分∠BDC,则t的值为 s;
(2)如图2,连接CM,设△CMQ的面积为S,求S关于t的函数关系式;
(3)在运动过程中,当t为何值时,⊙O与MN第一次相切?
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源:北师大版七年级数学下2.3.1 平行线的性质 同步练习 题型:单选题
如图,直线a∥b,∠1 = 60°,∠2 = 40°,则∠3等于( )
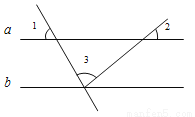
A. 40° B. 60° C. 80° D. 100°.
C 【解析】试题分析:根据平行线的性质:两直线平行,同位角相等,可知∠1=∠5=60°,∠2=∠4=40°,可求然后根据平角的定义可求∠3=180°-60°-40°=80°. 故选C查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册 第一章 整式的乘除 整式的运算 专题练习题 含答案 题型:解答题
计算:(-2a2)·(3ab2-5ab3)
-6a3b2+10a3b3 【解析】试题分析:同底数幂的乘法法则,底数不变,指数相加.根据单项式乘以多项式的计算法则得出答案. 试题解析:原式=-6a3b2+10a3b3.查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:填空题
已知x=1是方程x2-4x+c=0的一个根,则c的值是_________.
3 【解析】试题分析:把x=2代入x2-4x+c=0,得22-4×2+c=0, 解得c=4.查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:单选题
从一块正方形铁皮的四角上各剪去一个边长为3cm的小正方形,制成一个无盖的盒子,若盒子的容积为300cm3,则铁皮的边长为( )
A. 16cm B. 14cm C. 13cm D. 11cm
A 【解析】设正方形铁皮的边长应是x厘米,则做成没有盖的长方体盒子的长、宽为(x-3×2)厘米,高为3厘米,根据长方体的体积计算公式列方程解答即可. 【解析】 设正方形铁皮的边长应是x厘米,则没有盖的长方体盒子的长、宽为(x?3×2)厘米,高为3厘米,根据题意列方程得, (x?3×2)(x?3×2)×3=300, 解得x1=16,x2=?4(不合题意,舍去); 答:...查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年九年级(上)期末数学试卷 题型:解答题
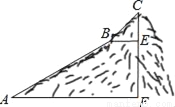
如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF(结果保留根式).
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年九年级(上)期末数学试卷 题型:填空题
一组射击运动员的测试成绩如下表:则中位数是_____.
成绩 | 6 | 7 | 8 | 9 | 10 |
次数 | 1 | 2 | 4 | 5 | 2 |
查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册第一章整式乘法1.7整式的除法课时练习 题型:解答题
(2a4 -6a2+4a) ÷ 2a
a3 -3a+2 【解析】试题分析:由多项式除以单项式法则与同底数幂的除法法则计算,即可完成此题. 试题解析:(2a4 -6a2+4a) ÷ 2a=2a4 ÷ 2a - 6a2÷ 2a +4a ÷ 2a = a3 -3a+2.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版5.1相交线同步练习 题型:填空题
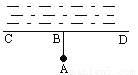
如图,计划把河水引到水池A中,先引AB⊥CD,垂足为B,然后 沿AB开渠,能使所开的渠道最短, 这样设计的依据是_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com