
��һ����������Ƥ���Ľ��ϸ���ȥһ���߳�Ϊ3cm��С�����Σ��Ƴ�һ���ǵĺ��ӣ������ӵ��ݻ�Ϊ300cm3������Ƥ�ı߳�Ϊ�� ��
A. 16cm B. 14cm C. 13cm D. 11cm
A ������������������Ƥ�ı߳�Ӧ��x���ף�������û�иǵij�������ӵij�����Ϊ��x-3��2�����ף���Ϊ3���ף����ݳ������������㹫ʽ�з��̽�ɣ� �������� ����������Ƥ�ı߳�Ӧ��x����,��û�иǵij�������ӵij�����Ϊ(x?3��2)���ף���Ϊ3���ף����������з��̵ã� (x?3��2)(x?3��2)��3=300�� ���x1=16,x2=?4(��������,��ȥ)�� ��... Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��2.3.1 ƽ���ߵ����� ͬ����ϰ ���ͣ���ѡ��
��ͼ��ֱ��l1��l2��CD��AB�ڵ�D����1=50�㣬���BCD�Ķ���Ϊ��������
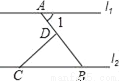
A. 50�� B. 45�� C. 40�� D. 30��
C ���������������������ƽ���ߵ����ʣ���֪��1=��B=50�㣬Ȼ�����ֱ�������ε�����ǻ��࣬�ɵá�BCD=90��-50��=40��. ��ѡ��C.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ�²� ��һ�¡���ʽ�ij˳� ��ʽ������ ר����ϰ�� ���� ���ͣ������
�Ȼ�������ֵ��[(x��2y2)2��(x��y2)(x��y2)��5y4]��2y������x����2��y��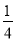
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ��ʦ����ϲ� ȫ���ۺϲ��Ծ�2 ���ͣ������
��ͼ��������ֽƬABCD�ı߳�Ϊ12��E��F�ֱ��DZ�AD��BC�ϵĵ㣬��������ֽƬ��EF�۵���ʹ�õ�A����CD���ϵĵ�A�䴦����ʱ��B���ڵ�B�䴦����֪�ۺ�EF=13����AE�ij�����_________��
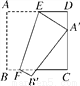
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ��ʦ����ϲ� ȫ���ۺϲ��Ծ�2 ���ͣ���ѡ��
У�˶����ϼס��ҡ�����������ѡ�ֲμ�100������������1�š�2�š�3�š�4��4���ܵ������ѡ���������ǩ�ķ�ʽ�������Ե��ܵ�����׳鵽1���ܵ����ҳ鵽2���ܵ��ĸ����ǣ� ��
A. 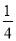 B.
B. 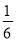 C.
C. 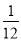 D.
D. 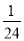
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�������żҸ���2016-2017ѧ����꼶���ϣ���ĩ��ѧ�Ծ� ���ͣ������
��ͼ���ھ���ABCD�У�AB=6cm��AD=8cm����P�ӵ�B�������ضԽ���BD���D�����˶����ٶ�Ϊ4cm/s������P��PQ��BD��BC�ڵ�Q����PQΪһ����������PQMN��ʹ�õ�N��������PD�ϣ���O�ӵ�D��������DC���C�����˶����ٶ�Ϊ3cm/s����OΪԲ�ģ�1cm�뾶����O����P���Dͬʱ�����������ǵ��˶�ʱ��Ϊt����λ��s�� ��0��t��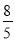 ����
����
��1����ͼ1������DQ����DQƽ�֡�BDC����t��ֵΪ�� ��s��
��2����ͼ2������CM�����CMQ�����ΪS����S����t�ĺ�����ϵʽ��
��3�����˶������У���tΪ��ֵʱ����O��MN��һ�����У�
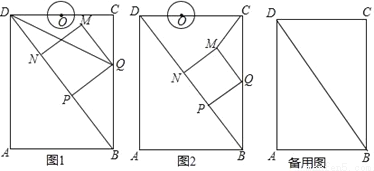
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�������żҸ���2016-2017ѧ����꼶���ϣ���ĩ��ѧ�Ծ� ���ͣ������
��֪����ABC��ֱ������ƽ���ڣ��������������ֱ�ΪA��0��3����B��3��4����C��2��2����������������ÿ��С�����εı߳���һ����λ���ȣ���
��1���Ե�BΪλ�����ģ��������ڻ�����A1B1C1��ʹ��A1B1C1���ABCλ�ƣ���λ�Ʊ�Ϊ2��1��
��2����C1���������� ������ ������
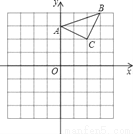
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�������żҸ���2016-2017ѧ����꼶���ϣ���ĩ��ѧ�Ծ� ���ͣ���ѡ��
���й���x�ķ�����ʵ�������ǣ�������
A. x2��x+1=0 B. x2+x+1=0 C. x2��x��1=0 D. ��x��1��2+1=0
C ������������������ֱ����A��B�е��б�ʽ��ֵ�������б�ʽ����������жϣ�������ʽ�ֽⷨ��C�����жϣ����ݷǸ��������ʶ�D�����жϣ� �������� A����=����1��2��4��1��1=��3��0������û��ʵ����������Aѡ����� B����=12��4��1��1=��3��0������û��ʵ����������Bѡ����� C��x��1=0��x+2=0����x1=1��x2=��2������Cѡ����ȷ�� D��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ�˽̰�5.1�ཻ��ͬ����ϰ ���ͣ������
��ͼ����ֱ֪��AB��CD�ཻ�ڵ�O��OEƽ�֡�AOC������OF��CD�ڵ�O���ҡ�BOF=32�㣬���COE�Ķ�����
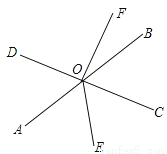
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com