练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    某段河流的两岸是平行的，数学兴趣小组在老师带领下不用涉水过河就测得河的宽度，他们是这样做的：

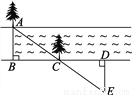
    ①在河流的一条岸边B点，选对岸正对的一棵树A；

    ②沿河岸直走20步有一棵树C，继续前行20步到达D处；

    ③从D处沿河岸垂直的方向行走，当到达A树正好被C树遮挡住的E处停止行走；

    ④测得DE的长就是河宽AB.

    请你说明他们做法的正确性．

    见解析 【解析】分析：将题目中的实际问题转化为数学问题，然后利用全等三角形的判定方法证得两个三角形全等即可说明其做法的正确性． 本题解析： ∵在△ABC和△EDC中，∠ABC=∠EDC=90°，BC=DC，∠ACB=∠ECD， ∴Rt△ABC≌Rt△EDC， ∴AB=ED， 即他们的做法是正确的.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版数学七年级下册第三章3.1用表格表示的变量间关系课时练习 题型：单选题

    弹簧挂上物体后会伸长，测得一弹簧的长度y（cm）与所挂的物体的质量x（kg）间有下面的关系：

    x

    0

    1

    2

    3

    4

    5

    y

    10

    10.5

    11

    11.5

    12

    12.5

    下列说法不正确的是（　　）

    A. x与y都是变量，且x是自变量，y是因变量

    B. 所挂物体质量为4kg时，弹簧长度为12cm

    C. 弹簧不挂重物时的长度为0cm

    D. 物体质量每增加1kg，弹簧长度y增加0.5cm

    D 【解析】A．x与y都是变量，且x是自变量，y是因变量，故A正确； B．所挂物体质量为4kg时，弹簧长度为12cm，故B正确； C．弹簧不挂重物时的长度为10cm，故C错误； D．物体质量每增加1kg，弹簧长度y增加0.5cm，故D正确． 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型：单选题

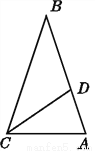
    如图,在△ABC中,BC=BA,点D在AB上,且AC=CD=DB,则图中的等腰三角形有(　　)

    A. 1个 B. 2个 C. 3个 D. 4个

    C 【解析】∵在△ABC中，BC=BA， ∴△ABC是等腰三角形； ∵点D在AB上，且AC=CD=DB， ∴△ACD和△BDC都是等腰三角形， 综上所述，图中共有三个等腰三角形. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型：填空题

    有一质地均匀的三角形铁片,若阿龙想用木棒撑住此铁片,则支撑点应设在该三角形的____处最恰当.

    重心 【解析】【解析】 有一质地均匀的三角形铁片，若阿龙想用木棒撑住此铁片，则支撑点应设在该三角形的重心处最恰当．故答案为：重心．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型：解答题

    如图，把一个三角板（AB=BC，∠ABC=90°）放入一个“U”形槽中，使三角板的三个顶点A、C、B分别在槽的两壁及底边上滑动，已知∠D=∠E=90°，在滑动过程中，你发现线段AD与BE有什么大小关系？试说明你的结论.

    ，见解析 【解析】【解析】 易发现AD与BE所在的△ABD与△BCE在滑动过程中始终全等，因而AD=BE．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型：单选题

    利用三角形全等测量距离的原理是( )

    A. 全等三角形对应角相等 B. 全等三角形对应边相等

    C. 大小和形状相同的两个三角形全等 D. 三边对应相等的两个三角形全等

    B 【解析】利用三角形全等测量距离，是指无法直接测量时，我们通过构造全等的方法，然后借助全等三角形对应边相等，间接测量距离，故选B.

    查看答案和解析>>

    科目：初中数学 来源：内蒙古包头市青山区2017-2018学年八年级（上）期末数学试卷 题型：填空题

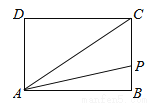
    如图，长方形ABCD中，AB=5，AD=3，点P从点A出发，沿长方形ABCD的边逆时针运动，设点P运动的距离为x；△APC的面积为y，如果5<x<8，那么y关于x的函数关系式为__________．

    y=–x+20 【解析】试题解析：当5＜x＜8时，点P在线段BC上，PC=8﹣x， ∴y=PC•AB=﹣x+20． 故答案为：y=﹣x+20．

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

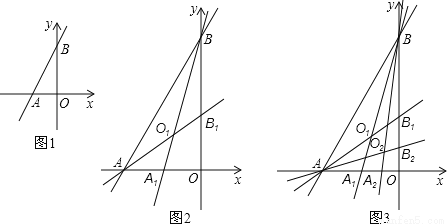
    如图1，一次函数y=2x+4与x轴，y轴分别相交于A，B两点，一次函数图象与坐标轴围成的△ABO，我们称它为此一次函数的坐标三角形．把坐标三角形面积分成相等的二部分的直线叫做坐标三角形的等积线．

    （1）求此一次函数的坐标三角形周长以及过点A的等积线的函数表达式；

    （2）如图2，我们把第一个坐标三角形△ABO记为第一代坐标三角形．第一代坐标三角形的等积线BA1，AB1记为第一对等积线，它们交于点O1，四边形A1OB1O1称为第一个坐标四边形．求点O1的坐标和坐标四边形A1OB1O1面积；

    （3）如图3．第一对等积线与坐标轴构成了第二代坐标三角形△BA1O．△AOB1分别过点A，B作一条平分△BA1O，△AOB1面积的第二对等积线BA2，AB2，相交于点O2，如此进行下去．…，请直接写出On的坐标和第n个坐标四边形面积（用n表示）．

    （1）周长为6+2；等积线的函数表达式：y=x+2；（2）；（3）. 【解析】试题分析：（1）令y=0求出x的值，令x=0求出x的值，从而得到点A、B的坐标，再求出OA、OB的长，然后利用勾股定理列式求出AB，再根据三角形的周长公式列式计算即可得解；根据等积线的定义求出A1、B1的坐标，然后利用待定系数法求一次函数解析式解答； （2）联立两等积线解析式求解即可得到O1的坐标，再根据坐标...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下5.3.1 等腰三角形的性质 同步练习 题型：单选题

    如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,下列结论:①∠BAD=∠CAD;②AD上任意一点到AB,AC的距离相等;③BD=CD;④若点P在直线AD上,则PB=PC.其中正确的是(　　)

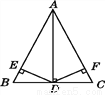
    A. ① B. ①② C. ①②③ D. ①②③④

    D 【解析】试题解析：∵AB=AC， ∴△ABC是等腰三角形， 又∵AD⊥BC于D， ∴∠BAD=∠CAD，BD=CD，故①③正确； ∵∠BAD=∠CAD， ∴AD上任意一点到AB、AC的距离相等，故②正确； ∵AD是BC的中垂线， ∴若点P在直线AD上，则PB=PC，故④正确. 故选D.

    查看答案和解析>>

    同步练习册答案