练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    弹簧挂上物体后会伸长，测得一弹簧的长度y（cm）与所挂的物体的质量x（kg）间有下面的关系：

    x

    0

    1

    2

    3

    4

    5

    y

    10

    10.5

    11

    11.5

    12

    12.5

    下列说法不正确的是（　　）

    A. x与y都是变量，且x是自变量，y是因变量

    B. 所挂物体质量为4kg时，弹簧长度为12cm

    C. 弹簧不挂重物时的长度为0cm

    D. 物体质量每增加1kg，弹簧长度y增加0.5cm

    D 【解析】A．x与y都是变量，且x是自变量，y是因变量，故A正确； B．所挂物体质量为4kg时，弹簧长度为12cm，故B正确； C．弹簧不挂重物时的长度为10cm，故C错误； D．物体质量每增加1kg，弹簧长度y增加0.5cm，故D正确． 故选：D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级数学下4.1.1 三角形及其内角和 同步练习 题型：单选题

    在一个直角三角形中，有一个锐角等于60°，则另一个锐角的度数是（ ）

    A. 120° B. 90° C. 60° D. 30°

    D 【解析】试题分析：根据直角三角形两锐角互余列式计算即可得【解析】 ∵直角三角形中，一个锐角等于60°，∴另一个锐角的度数=90°﹣60°=30°． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册4.3.2探索三角形全等的条件练习 题型：解答题

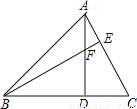
    如图，在△ABC中，AD⊥BC，BE⊥AC，AD=BD，求证：BF=AC。

    证明见解析 【解析】分析：先证出∠DBF=∠DAC,再由ASA证明△BDF≌△ADC,得出对应边相等即可. 本题解析： ∵AD⊥BC，BE⊥AC， ∴∠BDF=∠ADC=∠BEC=90°， ∴∠DBF+∠C=90°，∠DAC+∠C=90°， ∴∠DBF=∠DAC， 在△BDF和△ADC中， ∴△BDF≌△ADC（ASA）， ∴BF=AC。

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第三章3.1用表格表示的变量间关系课时练习 题型：填空题

    表示变量之间关系的常用方法有______，______，______．

    解析式 表格法 图象法 【解析】根据函数的定义，可得函数的表示方法有：解析式、表格法、图象法. 故答案为：(1). 解析式 (2). 表格法 (3). 图象法

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第三章3.1用表格表示的变量间关系课时练习 题型：单选题

    在三角形面积公式S=ah，a=2cm中，下列说法正确的是（　　）

    A. S，a是变量，h是常量 B. S，h是变量，是常量

    C. S，h是变量，a是常量 D. S，h，a是变量，是常量

    C 【解析】在三角形面积公式S=ah，a=2cm中，a是常数，h和S是变量． 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：北师大七年级下1.7 整式的除法 同步练习含答案 题型：解答题

    观察下列各式:

    (x-1)÷(x-1)=1;

    (x2-1)÷(x-1)=x+1;

    (x3-1)÷(x-1)=x2+x+1;

    (x4-1)÷(x-1)=x3+x2+x+1.

    (1)根据上面各式的规律可得(xn+1-1)÷(x-1)=　　　　; 

    (2)利用(1)的结论求22 017+22 016+…+2+1的值;

    (3)若1+x+x2+…+x2 017=0,求x2 018的值.

    (1) xn+xn-1+xn-2+…+x+1；（2）22 018-1.（3）1. 【解析】试题分析：(1)根据已知发现结果的规律:按x进行降幂排列,各项系数为1,直接写出结论即可; (2)将(1)中的规则逆用,计算即可; (3)将(1)中结论逆用,列出方程,求解即可. 解:(1)xn+xn-1+xn-2+…+x+1 (2)22 017+22 016+…+2+1 =(...

    查看答案和解析>>

    科目：初中数学 来源：北师大七年级下1.7 整式的除法 同步练习含答案 题型：解答题

    计算:(-2x2y+6x3y4-2xy)÷(-2xy).

    x-3x2y3+1. 【解析】试题分析：用多项式-2x2y+6x3y4-2xy中的每一项分别除以单项式-2xy，再把所得的商相加． 解:原式=x-3x2y3+1.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型：单选题

    在等腰△ABC中，AB=AC，其周长为20cm，则AB边的取值范围是（ ）

    A. 1cm＜AB＜4cm B. 5cm＜AB＜10cm

    C. 4cm＜AB＜8cm D. 4cm＜AB＜10cm

    B 【解析】试题分析：∵在等腰△ABC中，AB=AC，其周长为20cm，∴设AB="AC=x" cm，则BC=（20﹣2x）cm，∴，解得5cm＜x＜10cm．故选B．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型：解答题

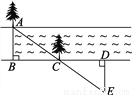
    某段河流的两岸是平行的，数学兴趣小组在老师带领下不用涉水过河就测得河的宽度，他们是这样做的：

    ①在河流的一条岸边B点，选对岸正对的一棵树A；

    ②沿河岸直走20步有一棵树C，继续前行20步到达D处；

    ③从D处沿河岸垂直的方向行走，当到达A树正好被C树遮挡住的E处停止行走；

    ④测得DE的长就是河宽AB.

    请你说明他们做法的正确性．

    见解析 【解析】分析：将题目中的实际问题转化为数学问题，然后利用全等三角形的判定方法证得两个三角形全等即可说明其做法的正确性． 本题解析： ∵在△ABC和△EDC中，∠ABC=∠EDC=90°，BC=DC，∠ACB=∠ECD， ∴Rt△ABC≌Rt△EDC， ∴AB=ED， 即他们的做法是正确的.

    查看答案和解析>>

    同步练习册答案