
关于x的一元二次方程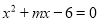 的一个根的值为3,则另一个根的值是_____.
的一个根的值为3,则另一个根的值是_____.
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(一) 题型:单选题
如图,在△ACB中,∠ACB=100°,∠A=20°,D是AB上一点.将△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于( )
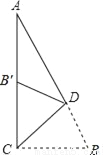
A. 25° B. 30° C. 35° D. 40°
D 【解析】∵在△ACB中,∠ACB=100°,∠A=20°,∴∠B=180°-100°-20°=60°, ∵△CDB′由△CDB翻折而成,∴∠CB′D=∠B=60°, ∵∠CB′D是△AB′D的外角,∴∠ADB′=∠CB′D-∠A=60°-20°=40°. 故选D.查看答案和解析>>
科目:初中数学 来源:湖南省新化县2016-2017学年度第二学期期中检测七年级数学试卷 题型:填空题
因式分【解析】
2a2 – 8 = _______________.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
如图,AB是⊙O的直径,C是⊙O上一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.求证:MN是⊙O的切线.
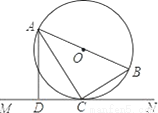
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:填空题
某校要从四名学生中选拔一名参加“汉字听写”大赛,选择赛中每名学生的平均学生的平均成绩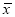 及其方差
及其方差 如表所示,如果要选一名成绩高且发挥稳定的学生参赛,则应选择的学生是___.
如表所示,如果要选一名成绩高且发挥稳定的学生参赛,则应选择的学生是___.
甲 | 乙 | 丙 | 丁 | |
| 8 | 9 | 9 | 8 |
| 1 | 1 | 1.2 | 1.3 |
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:单选题
如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )
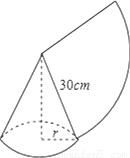
A. 5cm B. 10cm C. 20cm D. 5πcm
B 【解析】试题分析:圆锥的底面周长=扇形的弧长,据此列等式求出r的值. ,解得r=10cm. 故答案为:10cm.查看答案和解析>>
科目:初中数学 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:解答题
如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.
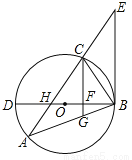
(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BG•BA=48,FG=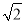 ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
查看答案和解析>>
科目:初中数学 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:填空题
据统计,参加今年扬州市初中毕业、升学统一考试的学生约36800人,这个数据用科学记数法表示为_________。
3.68×104 【解析】 .查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
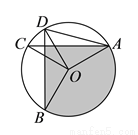
如图,在⊙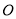 中,弦
中,弦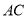 ,
, 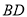 相交于点
相交于点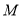 ,且
,且 .
.
( )求证:
)求证: 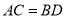 ;
;
( )若
)若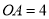 ,
, 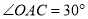 ,当
,当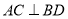 时,求:
时,求:
①图中阴影部分面积.
②弧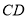 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com