练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

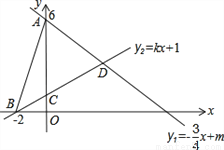
    如图，直线l1：y1=?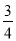x+m与y轴交于点A（0，6），直线l2：y2=kx+1分别与x轴交于点B（-2，0），与y轴交于点C．两条直线相交于点D，连接AB．

    （1）求两直线交点D的坐标；

    （2）求△ABD的面积；
    （3）根据图象直接写出y1＞y2时自变量x的取值范围．

    （1）D点坐标为（4，3）（2）15；（3）x＜4 【解析】试题分析：（1）先得到两函数的解析式，组成方程组解求出D的坐标；（2）由y2= x+1可知，C点坐标为（0，1），分别求出△ABC和△ACD的面积，相加即可．（3）由图可直接得出y1＞y2时自变量x的取值范围． 试题解析：（1）将A（0，6）代入y1=?x+m得，m=6；将B（-2，0）代入y2=kx+1得，k= ...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖北省襄阳市襄城区2016-2017学年度上学期期末考试八年级数学试卷 题型：填空题

    当x=2016时,分式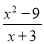的值＝___________.

    2013 【解析】试题解析：当x=2016时，分式=x-3， 则原式=2016-3=2013． 故答案为：2013．

    查看答案和解析>>

    科目：初中数学 来源：2017年山东省枣庄市中考数学模拟试卷 题型：解答题

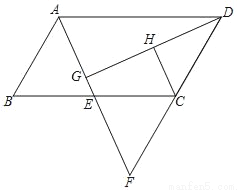
    如图，四边形ABCD为平行四边形，E为BC的中点，连接AE并延长交DC的延长线于点F．

    （1）求证：△ABE≌△FCE；

    （2）过点D作DG⊥AE于点G，H为DG的中点．判断CH与DG的位置关系，并说明理由．

    （1）证明见解析; （2）CH⊥DG．理由见解析. 【解析】（1）根据平行四边形的性质得到两角一边对应相等，利用AAS判定△ABE≌△FCE； （2）易证CH为ΔDGF的中位线，所以CH∥GF，由DG⊥AE可得CH⊥DG． 试题解析：（1）∵四边形为平行四边形 ∴∥， ∴ ∵为的中点 ∴ ∵ ∴△≌△ （2） ∵△≌△ ∴ ...

    查看答案和解析>>

    科目：初中数学 来源：2017年山东省枣庄市中考数学模拟试卷 题型：单选题

    二次函数y=ax2+bx+c的图象如图所示，对称轴是直线x=﹣1，有以下结论：①abc＞0；②4ac＜b2；③2a+b=0；④a﹣b+c＞2．其中正确的结论的个数是（　　）

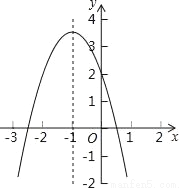
    A. 1 B. 2 C. 3 D. 4

    C 【解析】①∵抛物线开口向下，∴a＜0，∵抛物线的对称轴为直线x==﹣1，∴b=2a＜0，∵抛物线与y轴的交点在x轴上方，∴c＞0，∴abc＞0，所以①正确； ②∵抛物线与x轴有2个交点，∴△=b2-4ac＞0，∴4ac

    查看答案和解析>>

    科目：初中数学 来源：2017年山东省枣庄市中考数学模拟试卷 题型：单选题

    下列计算正确的是（　　）

    A. 2a﹣a=1 B. a2+a2=2a4 C. a2•a3=a5 D. （a﹣b）2=a2﹣b2

    C 【解析】试题分析：A.2a﹣a=a，故错误； B．a2+a2=2a2，故错误； C．a2•a3=a5，正确； D．（a﹣b）2=a2﹣2ab+b2，故错误； 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年内蒙古鄂尔多斯市鄂托克旗八年级（下）期末数学试卷 题型：填空题

    如图，O为数轴原点，A，B两点分别对应－3，3，作腰长为4的等腰△ABC，连接OC，以O为圆心，CO长为半径画弧交数轴于点M，则点M对应的实数为__________ ．

    【解析】试题分析：根据题意得，等腰△ABC中，OA=OB=3,由等腰三角形的性质可得OC⊥AB，根据勾股定理可得OC=，又因OM=OC=，于是可确定点M对应的数为．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年内蒙古鄂尔多斯市鄂托克旗八年级（下）期末数学试卷 题型：单选题

    如图，四边形ABCD是菱形，对角线AC，BD相交于点O，DH⊥AB于H，连接OH，∠DHO=20°，则∠CAD的度数是（　　）

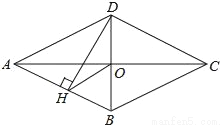
    A. 20° B. 25° C. 30° D. 40°

    A 【解析】试题解析：∵四边形ABCD是菱形， ∴OB=OD，AC⊥BD， ∵DH⊥AB， ∴OH=OB=BD， ∵∠DHO=20°， ∴∠OHB=90°-∠DHO=70°， ∴∠ABD=∠OHB=70°， ∴∠CAD=∠CAB=90°-∠ABD=20°． 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省武汉市中考数学模拟试卷二 题型：填空题

    小李不慎将墨水滴在数轴上，根据图中的数值，判断墨迹盖住的整数有_____个．

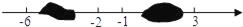
    6 【解析】-6到-2之间的整数个数有3个，-1到3之间的整数个数有3个，共有6个. 故答案为6.

    查看答案和解析>>

    科目：初中数学 来源：四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型：解答题

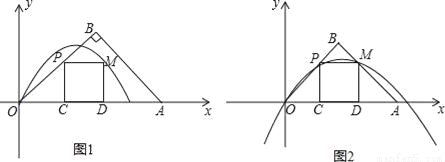
    如图1在平面直角坐标系中．等腰Rt△OAB的斜边OA在x轴上．P为线段OB上﹣动点（不与O，B重合）．过P点向x轴作垂线．垂足为C．以PC为边在PC的右侧作正方形PCDM．OP=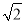t，OA=3．设过O，M两点的抛物线为y=ax2+bx．其顶点N（m，n）

    （1）写出t的取值范围　　，写出M的坐标：（　　，　　）；

    （2）用含a，t的代数式表示b；

    （3）当抛物线开向下，且点M恰好运动到AB边上时（如图2）

    ①求t的值；

    ②若N在△OAB的内部及边上，试求a及m的取值范围．

    （1）0＜t＜，M（2t，t）；（2）b=；（3）①t=1；②≤m≤2． 【解析】试题分析： 试题解析：(1)如图1，∵△OAB为等腰直角三角形，OA=3， ∵P为线段OB上?动点(不与O,B重合)， ∵四边形PCDM为正方形， ∴△POC为等腰直角三角形， ∴PC=OC=t， ∴OD=t+t=2t， ∴M(2t,t)； (2)把M(2t,t)...

    查看答案和解析>>

    同步练习册答案