
解方程:x2+2x-1=0.
x1=-1+,x2=-1-. 【解析】利用公式法即可求解. 【解析】 ∵a=1,b=2,c=-1, ∴b2-4ac=22-4×1×(-1)=8, ∴x=, 即x1=-1+,x2=-1-. 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源:北师大版七年级下册1.3.1同底数幂的除法 练习题 题型:单选题
下列运算正确的是( )
A. (-2)0=-2 B. (-x)3÷(-x)2=x C. (-1)-2=-1 D. (-1)0=1
D 【解析】选项A,(-2)0=1;选项B,(-x)3÷(-x)2=-x;选项C,(-1)-2=1;选项D,(-1)0=1.故选D.查看答案和解析>>
科目:初中数学 来源:北师大版 七年级数学下册 第一章 整式的乘除 单项式与多项式相乘 专题练习题 含答案 题型:单选题
某圆柱体的底面直径和高如图所示,则这个圆柱体的表面积为( )
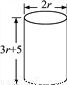
A. 7πr2+10πr B. 8πr2+10πr C. 8πr2+20πr D. 6πr2+10πr
B 【解析】试题分析:圆柱体的表面积等于侧面积加上两个底面的面积.则S= ,故选B.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册 第一章 整式的乘除 整式的运算 专题练习题 含答案 题型:解答题
计算:12x7y6z2÷(-3x3y2)2÷(-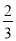 y)
y)
查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:解答题
数学活动——探究特殊的平行四边形.
问题情境
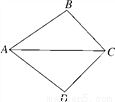
如图,在四边形ABCD中,AC为对角线,AB=AD,BC=DC.请你添加条件,使它们成为特殊的平行四边形.
提出问题
(1)第一小组添加的条件是“AB∥CD”,则四边形ABCD是菱形.请你证明;
(2)第二小组添加的条件是“∠B=90°,∠BCD=90°”,则四边形ABCD是正方形.请你证明.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:填空题
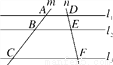
如图,已知直线l1∥l2∥l3,分别交直线m,n于点A,D,B,E,C,F,AB=5cm,AC=15cm,DE=3cm,则EF的长为________cm.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:单选题
一次函数y=ax-a与反比例函数y=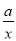 (a≠0)在同一平面直角坐标系中的图象可能是( )
(a≠0)在同一平面直角坐标系中的图象可能是( )
A. 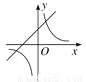 B.
B. 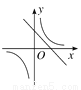 C.
C. 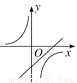 D.
D. 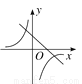
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年九年级(上)期末数学试卷 题型:填空题
圆锥的母线长5cm,底面半径长3cm,那么它的侧面展开图的圆心角是 度.
216°. 【解析】 试题分析:易得圆锥的底面周长,也就是圆锥侧面展开图的弧长,利用弧长公式即可求得侧面展开图的圆心角. 试题解析:∵圆锥的底面半径长3cm, ∴圆锥的底面周长为6πcm, 设扇形的圆心角为n°, ∴, 解得n=216°.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下3.1 用表格表示的变量间关系 同步练习 题型:解答题
心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:min)之间有如下关系(其中0≤x≤20):
提出概念所 用时间x/min | 2 | 5 | 7 | 10 | 12 | 13 | 14 | 17 | 20 |
对概念的接 受能力y | 47.8 | 53.5 | 56.3 | 59 | 59.8 | 59.9 | 59.8 | 58.3 | 55 |
(注:接受能力值越大,说明学生的接受能力越强)
(1)上表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当提出概念所用时间是10 min时,学生的接受能力是多少?
(3)根据表格中的数据,你认为提出概念所用时间为多少时,学生的接受能力最强?
(4)从表格中可知,当提出概念所用时间x在什么范围内时,学生的接受能力逐步增强?当提出概念所用时间x在什么范围内时,学生的接受能力逐步降低?
(1)反映了提出概念所用的时间x和对概念的接受能力y两个变量之间的关系;其中x是自变量,y是因变量. (2) 59. (3)所用时间为13 min时,学生的接受能力最强. (4)当x在2至13的范围内,学生的接受能力逐步增强;当x在13至20的范围内,学生的接受能力逐步降低. 【解析】分析:(1)由条件可知两个变量是提出概念所用的时间和对概念的接受能力,对概念的接受能力随着...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com