
说明:在解答“结论应用”时,从(A),(B)两题中任选一题作答.
问题探究
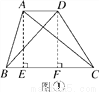
启知学习小组在课外学习时,发现了这样一个问题:如图①,在四边形ABCD中,连接AC,BD,如果△ABC与△BCD的面积相等,那么AD∥BC.在小组交流时,他们在图①中添加了如图所示的辅助线,AE⊥BC于点E,DF⊥BC于点F.请你完成他们的证明过程.
结论应用
在平面直角坐标系中,反比例函数y=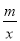 (x≠0)的图象经过A(1,4),B(a,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D.
(x≠0)的图象经过A(1,4),B(a,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D.
(A)(1)求反比例函数的表达式;
(2)如图②,已知b=1,AC,BD相交于点E,求证:CD∥AB.
(B)(1)求反比例函数的表达式;
(2)如图③,若点B在第三象限,判断并证明CD与AB的位置关系.
我选择:__________.
 计算高手系列答案
计算高手系列答案科目:初中数学 来源:北师大版七年级下册1.3.1同底数幂的除法 练习题 题型:解答题
计算:xm•(xn)3÷(xm-1•2xn-1).
0.5x2n+2 【解析】试题分析:先根据幂的乘方的运算法则进行乘方运算,再根据同底数幂的乘法法则和除法法则进行计算即可. 试题解析: 原式=xm•x3n÷(2xm-1+n-1), =xm+3n÷2xm+n-2, =0.5x2n+2.查看答案和解析>>
科目:初中数学 来源:北师大版 七年级数学下册 第一章 整式的乘除 单项式与单项式相乘 专题练习题 含答案 题型:单选题
计算(5×103)(7×104)的正确结果是( )
A. 35×107 B. 3.5×108 C. 0.35×109 D. 3.5×107
B 【解析】试题分析:同底数幂的乘法法则:底数不变,指数相加.原式=,故选B.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册 第一章 整式的乘除 整式的运算 专题练习题 含答案 题型:解答题
已知m2+m-1=0,求m3+2m2+2017的值.
2018 【解析】试题分析:首先根据题意得出,然后将所求的代数式化简成,然后利用整体代入的思想进行求值. 试题解析:由m2+m-1=0,得m2+m=1, 原式=m3+m2+m2+2017=m(m2+m)+m2+2017=m2+m+2017=1+2017=2018.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册 第一章 整式的乘除 整式的运算 专题练习题 含答案 题型:解答题
计算:12x7y6z2÷(-3x3y2)2÷(-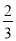 y)
y)
查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:解答题
如图,在?ABCD中,对角线AC与BD相交于点O,△ABO是等边三角形,AB=4,求BC的长.
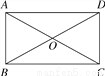
查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:填空题
如图,已知直线l1∥l2∥l3,分别交直线m,n于点A,D,B,E,C,F,AB=5cm,AC=15cm,DE=3cm,则EF的长为________cm.
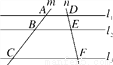
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年九年级(上)期末数学试卷 题型:解答题
已知二次函数y=﹣x2+2x+3.
(1)画出这个函数的图象;
(2)根据图象,直接写出;
①当函数值y为正数时,自变量x的取值范围;
②当﹣2<x<2时,函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册第一章整式乘法1.7整式的除法课时练习 题型:单选题
(x17y+x14z)÷(-x7)2 等于( )
A. x3y+z B. -xy3+z C. -x17y+z D. xy+z
A 【解析】(x17y+x14z)÷(-x7)2=(x17y+x14z)÷x14=x17y÷x14+x14z÷x14= x3y+z, 故选:A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com