练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠EFB=65°，则∠AED′等于（ ）

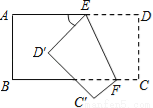
    A. 70° B. 65° C. 50° D. 25°

    C 【解析】试题分析：由平行可求得∠DEF，又由折叠的性质可得∠DEF=∠D′EF，结合平角可求得∠AED′．∵四边形ABCD为矩形，∴AD∥BC，∴∠DEF=∠EFB=65°，又由折叠角相等可得∠D′EF=∠DEF=65°，∴∠AED′=180°﹣65°﹣65°=50°，故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版初中数学七年级下册第五章《相交线与平行线--垂线》同步练习 题型：单选题

    点到直线的距离是指这点到这条直线的( )

    A. 垂线段 B. 垂线 C. 垂线的长度 D. 垂线段的长度

    D 【解析】试题解析：根据定义，点到直线的距离是指这点到这条直线的垂线段的长度. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：2018届中考数学专题复习同步练习题：一次函数 题型：填空题

    如图,直线y＝kx＋b经过A（－2，－1）和B（－3，0）两点,则不等式－3≤－2x－5＜kx＋b的解集是_______________。

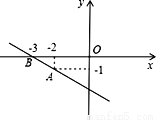
    -2＜x≤-1 【解析】解:因为直线y＝kx＋b经过A（－2，－1）和B（－3，0）， 所以，解得， 不等式变为-3≤-2x-5<-x-3, 解得-2

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年人教版七年级数学第五章相交线与平行线单元测试 题型：解答题

    如图，M，N为坐落于公路两旁的村庄，如果一辆施工的机动车由A向B行驶，产生的噪音会对两个村庄造成影响．

    (1)当施工车行驶到何处时，产生的噪音分别对两个村庄影响最大？在图中标出来．

    (2)当施工车从A向B行驶时，产生的噪音对M，N两个村庄的影响情况如何？

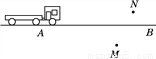
    见解析 【解析】试题分析：（1）过点M，N分别作AB的垂线，垂足分别为P，Q，根据垂线段最短可得汽车行驶到何处时，分别对两所学校影响最大； （2）此题说明时要分3段A到P；由P向Q，由Q 向B分别说明对两学校的影响情况． 试题解析： 【解析】 （1）如图所示，过点M，N分别作AB的垂线，垂足分别为P，Q，则当施工车行驶到点P，Q处时产生的噪音分别对M，N两个村庄影响最大．...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年人教版七年级数学第五章相交线与平行线单元测试 题型：单选题

    下列说法正确的是（ ）

    A. 有且只有一条直线与已知直线平行

    B. 垂直于同一条直线的两条直线互相平行

    C. 从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离

    D. 在平面内过一点有且只有一条直线与已知直线垂直

    D 【解析】试题分析：A、B两个缺少在同一平面内这个大前提条件；C、从直线外一点到这条直线的垂线段的长度，叫做这点到这条直线的距离.

    查看答案和解析>>

    科目：初中数学 来源：人教版初中数学九年级上册第二十一章《配方法解一元二次方程》练习题 题型：解答题

    用配方法说明下列结论：

    （1）代数式x2+8x+17的值恒大于0；

    （2）代数式2x-x2-3的值恒小于0

    （1）代数式x2+8x+17的值恒大于0（2）代数式2x-x2-3的值恒小于0 【解析】试题分析：运用配方法的运算方法，第一步：如果二次项数不是1，首先提取二次项系数，一次项与二次项都提取二次项系数并加括号，常数项可以不参与运算；第二步：配方，加常数项为一次项系数一半的平方，注意括号外应相应的加减这个常数项，保证配方后不改变原式的值，分别进行运算即可． 试题解析：【解析】 （1）x2...

    查看答案和解析>>

    科目：初中数学 来源：人教版初中数学九年级上册第二十一章《配方法解一元二次方程》练习题 题型：单选题

    若x2+6x+m2是一个完全平方式，则m的值为（ ）

    A. 3 B. -3 C. ±3 D. 以上都不对

    C 【解析】【解析】 ∵x2+2mx+m2=（x+m）2，∴在x2+6x+m2中，6x=±2mx，m=±3．故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版上册：第2章 整式的加减 单元测试卷 题型：填空题

    若多项式的一次项系数是－5，二次项系数是8，常数项是－2，且只含一个字母x，请写出这个多项式________.

    8x2－5x－2 【解析】由题意得，这个多项式是8x2－5x－2.

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级下册数学 第18章 平行四边形 单元检测卷 题型：解答题

    如图，在?ABCD中，BD是对角线，AE⊥BD于点E，CF⊥BD于点F，试判断四边形AECF是不是平行四边形，并说明理由．

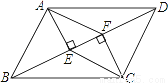
    见解析 【解析】试题分析：根据垂直，利用内错角相等两直线平行可得AE∥CF，在根据平行四边形的性质证明△ABE与△DCF全等，根据全等三角形对应边相等可得AE=CF，然后根据有一组对边平行且相等的四边形是平行四边形即可证明． 试题解析：四边形AECF是平行四边形，理由如下： ∵AE⊥BD于点E，CF⊥BD于点F， ∴∠AEF=∠CFE=90°， ∴AE∥CF（内错角相...

    查看答案和解析>>

    同步练习册答案