
据报道,春节期间微信红包收发高达3270000000次,数字3270000000用科学记数法表示为 _____
3.27×109. 【解析】试题分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.因此可求3270000000=3.27×109. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:甘肃省张掖市高台县2016-2017学年八年级(上)期末数学试卷 题型:单选题
一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米)与燃烧时间t(时)的函数关系的图象是( )
A. 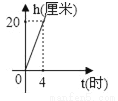 B.
B. 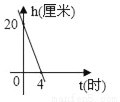
C. 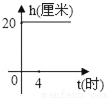 D.
D. 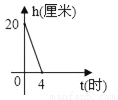
查看答案和解析>>
科目:初中数学 来源:重庆市江北区2018届九年级上期末模拟数学试卷 题型:填空题
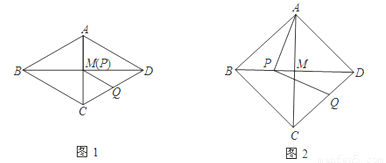
在△ABC中,BA=BC,∠BAC=α,M是AC的中点,P是线段BM上的动点,将线段PA绕点P顺时针旋转2α得到线段PQ.
(1)若α=60°,且点P与点M重合(如图1),线段CQ的延长线交射线BM于点D,此时∠CDB的度数为________
(2)在图2中,点P不与点B、M重合,线段CQ的延长线交射线BM于点D,则∠CDB的度数为(用含α的代数式表示)________ .
(3)对于适当大小的α,当点P在线段BM上运动到某一位置(不与点B、M重合)时,能使得线段CQ的延长线与射线BM交于点D,且PQ=DQ,则α的取值范围是________
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(三) 题型:解答题
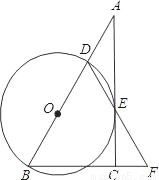
如图,在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长,与BC的延长线交于点F.
(1)求证:BD=BF;
(2)若BC=6,AD=4,求sinA的值.
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(三) 题型:填空题
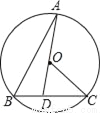
如图,BC是⊙O弦,D是BC上一点,DO交⊙O于点A,连接AB、OC,若∠A=20°,∠C=30°,则∠AOC的度数为_____.
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(三) 题型:单选题
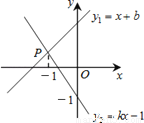
如图,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是( )
A. 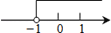 B.
B. 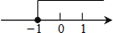 C.
C. 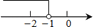 D.
D. 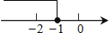
查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市资兴市兴华实验学校中考数学模拟试卷 题型:解答题
(12分)如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线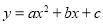 过点D,B,C三点.
过点D,B,C三点.
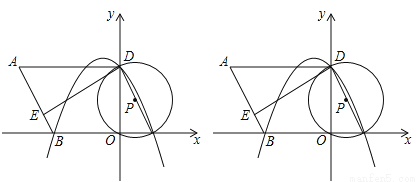
(1)求抛物线的解析式;
(2)求证:ED是⊙P的切线;
(3)若将△ADE绕点D逆时针旋转90°,E点的对应点E′会落在抛物线 上吗?请说明理由;
上吗?请说明理由;
(4)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
(1);(2)证明见试题解析;(3)不在;(4)N(﹣5,)或(3,)或(﹣3,). 【解析】 试题分析:(1)先确定点B的坐标,再在Rt△OCD中利用∠OCD的正切求出OD的长,从而得到点D的坐标,然后利用交点式求抛物线的解析式; (2)先计算出CD=2OC=4,由平行四边形的性质得到AB=CD=4,AB∥CD,∠A=∠BCD=60°,AD=BC=6,则由AE=3BE得到AE=...查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市资兴市兴华实验学校中考数学模拟试卷 题型:单选题
为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )
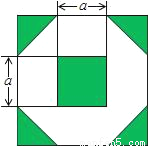
A. 2a2 B. 3a2 C. 4a2 D. 5a2
A 【解析】正多边形和圆,等腰直角三角形的性质,正方形的性质。图案中间的阴影部分是正方形,面积是,由于原来地砖更换成正八边形,四周一个阴影部分是对角线为的正方形的一半,它的面积用对角线积的一半来计算: 。故选A。查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:解答题
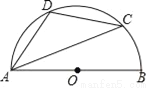
如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=20°,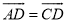 .请连结线段CB,求四边形ABCD各内角的度数.
.请连结线段CB,求四边形ABCD各内角的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com