
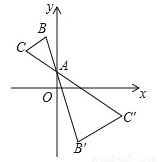
��ͼ��������ϵ�У���A��0��2��Ϊλ�����ģ���y���Ҳ�����ABC�Ŵ�2�����λ��ͼ�Ρ�AB'C'����C�Ķ�Ӧ��C'������Ϊ��m��n�������C������Ϊ��������
A. ��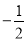 m��
m�� 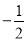 n+3�� B. ��
n+3�� B. ��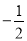 m��
m�� 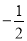 n��3��
n��3��
C. ��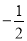 m��
m�� 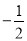 n+2�� D. ��
n+2�� D. ��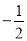 m��
m�� 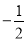 n��2��
n��2��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�����ɹų����������2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ʽ��4x2-2x+5=7����ʽ��2x2-x+1��ֵ���ڣ� ��
A. 2 B. 3 C. -2 D. 4
A �������������������4x2-2x+5=7�� ��4x2-2x=2�� ��2x2-x=1�� ��2x2-x+1=1+1=2�� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ����ĩģ����ѧ�Ծ� ���ͣ������
��ͼ��Բ�Ķ���x���������ϵİ�ԲO1����ԲO2��������ԲOn��ֱ��l���У����ԲO1����ԲO2��������ԲOn�İ뾶�ֱ���r1��r2������rn����ֱ��l��x���������Ϊ30�㣬��r1��1ʱ��r2018��_________.
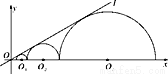
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017����꼶���ϣ���ĩ��ѧ�Ծ��������棩 ���ͣ������
��֪����y=��m+ ��x2+��2m��1��x��3����֤������mΪ��ֵ���ú���ͼ����x����н��㣮
��x2+��2m��1��x��3����֤������mΪ��ֵ���ú���ͼ����x����н��㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017����꼶���ϣ���ĩ��ѧ�Ծ��������棩 ���ͣ������
��������y1����ƽ��2����λ������ԭ����ת180��õ�������y2=2x2+4x+4����y1�Ľ���ʽΪ______��
y1=��2��x+1��2��2�� ����������y2=2x2+4x+4�� =2��x2+2x+1��+2�� =2��x+1��2+2�� ��������y2�Ķ�������Ϊ����1��2���� ��������y1����ƽ��2����λ����ԭ����ת180��õ�������y2�� ��������y1����ƽ��2����λ�Ķ�������Ϊ��1����2���� ��������y1����ƽ��2����λ�� ��������y1�Ķ�������Ϊ����1����2��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶����ѧ�ڶ��¡�һԪ���η��̡���Ԫ���� ���ͣ������
��ͼ���ھ���ABCD�У�BC��20 cm��P��Q��M��N�ֱ��A��B��C��D��������AD��BC��CB��DA�����ھ��εı���ͬʱ�˶�������һ�����ȵ��������˶��ߵ���һ���˵�ʱ���˶���ֹͣ����֪����ͬʱ���ڣ���BQ��x cm(x��0)����AP��2x cm��CM��3x cm��DN��x2 cm��
(1)��xΪ��ֵʱ����P��N�غϣ�
(2)��xΪ��ֵ�ǣ���P��Q��M��NΪ������ı�����ƽ���ı��Σ�
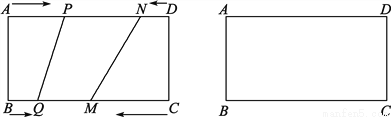
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶����ѧ�ڶ��¡�һԪ���η��̡���Ԫ���� ���ͣ������
�ֶ������㡰�����������ʵ��a��b������a��b=a2��3a+b���磺3��5=32��3��3+5����x��2=6����ʵ��x��ֵ��_______��
-1��4 ������������������������е��¶��彫����ʽ��ת��ΪһԪ���η��̣����һԪ���η��̵Ľ⼴�ɵõ�x��ֵ�� �������е��¶��彫x��2=6���εã� x2��3x+2=6����x2��3x��4=0�� ��ʽ�ֽ�ã���x��4����x+1��=0����ã�x1=4��x2=��1�� ��ʵ��x��ֵ�ǩ�1��4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�²ᣨ��ʦ��棩����ĩ����� ���ͣ������
��ͼ����?ABCD�У���ABC����BCD��ƽ����BE��CF�ֱ���AD�ཻ�ڵ�E��F��BE��CF�ཻ�ڵ�G.
(1)��֤��BE��CF��
(2)��AB��3��BC��5��CF��2����BE�ij���
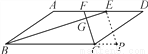
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������Դ��2016-2017ѧ����꼶����ĩ������ѧ�Ծ����� ���ͣ���ѡ��
ij��Ʒ���˶����������ν��ۣ�ÿ�����ۼ���560Ԫ��Ϊ315Ԫ����֪���ν��۵İٷ�����ͬ����ÿ�ν��۵İٷ��ʣ���ÿ�ν��۵İٷ���Ϊx���������еķ�������ȷ���ǣ�������
A. 560��1��x��2��315 B. 560��1��x��2��315
C. 560��1��2x��2��315 D. 560��1��x2����315
B ������������������������⣬����ÿ�ν��۵İٷ���Ϊx�����з���Ϊ560��1-x��²=315. ��ѡ��B�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com