练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，点A、B在函数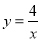（x＞0）的图象上，过点A、B分别向x、y轴作垂线，若阴影部分图形的面积恰好等于S1，则S1+S2=__________．

    4 【解析】∵S1=S阴影，S2+S阴影=4， ∴S1+S2=4.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型：单选题

    有理数m，n在数轴上的位置如图所示，则化简│n│-│m-n│的结果是（ ）

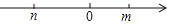
    A. m B. 2n-m C. -m D. m-2n

    C 【解析】根据数轴的特点，可知n＜0＜m，且|n|＞|m|，因此可知m-n＞0，所以根据绝对值的意义可知│n│-│m-n│=-n-m+n=-m. 故选：C.

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：解答题

    计算：

    （1）（﹣a2）3•4a （2）2x（x+1）+（x+1）2．

    (1)-4a7; (2) 3x2+4x+1． 【解析】试题分析:（1）根据幂的乘方、同底数幂的乘法进行计算即可； （2）根据单项式乘以多项式以及完全平方公式进行计算即可． 【解析】 （1）原式=﹣a6•4a =﹣4a7； （2）原式=2x2+2x+x2+2x+1 =3x2+4x+1．

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：解答题

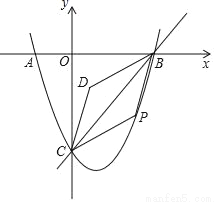
    如图，在平面直角坐标系中，抛物线y=x2+bx+c与x轴交于点A（﹣1，0），B（3，0），与y轴交于点C，作直线BC，点P是抛物线上一个动点（点P不与点B，C重合），连结PB，PC，以PB，PC为边作?CPBD，设?CPBD的面积为S，点P的横坐标为m．

    （1）求抛物线对应的函数表达式；

    （2）当点P在第四象限，且?CPBD有两个顶点在x轴上时，求点P的坐标；

    （3）求S与m之间的函数关系式；

    （4）当x轴将?CPBD的面积分成1：7两部分时，直接写出m的值．

    （1）y=x2﹣2x﹣3；（2）（2，﹣3）； （3）S=3m2﹣9m； （4）m的值为1或1+或1﹣． 【解析】试题分析：（1）利用交点式求抛物线的解析式； （2）先确定点D在x轴上，再利用平行四边形的性质可判断PC∥x轴，然后根据抛物线的对称性确定点P的坐标； （3）作PQ∥y轴交直线BC于Q，如图1，利用待定系数法求出直线BC的解析式为y=x-3，设P（m，m2-2m...

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：解答题

    小王每天乘公交车上班，车程为17.5千米，开设公交专用车道后，车程没变，公交车平均每小时比原来多行驶5千米，现在上班乘公交车所用时间是原来所用时间的，求小王原来上班乘公交车所需的时间．

    0.5小时 【解析】试题分析：设小王原来上班乘公交车所需的时间为x小时，则现在上班乘公交车所用时间是小时，根据公交车平均每小时比原来多行驶5千米，列方程求解． 【解析】 设小王原来上班乘公交车所需的时间为x小时，则现在上班乘公交车所用时间是x小时， 由题意得，﹣=5， 解得：x=0.5， 经检验，x=0.5是原方程的解． 答：小王原来上班乘公交车所需的时间为0...

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：单选题

    如图，四边形ABCD是⊙O的内接四边形，若∠B=80°，则∠ADC的度数是（　　）

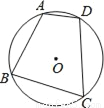
    A. 60° B. 80° C. 90° D. 100°

    D 【解析】∵四边形ABCD是⊙O的内接四边形， ∴∠ADC=180°-∠B=180°-80°=100°. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省平凉市中考数学模拟试卷 题型：解答题

    如图，抛物线y=ax2+2x﹣3与x轴交于A、B两点，且B（1，0）

    （1）求抛物线的解析式和点A的坐标；

    （2）如图1，点P是直线y=x上的动点，当直线y=x平分∠APB时，求点P的坐标；

    （3）如图2，已知直线y=x﹣分别与x轴、y轴交于C、F两点，点Q是直线CF下方的抛物线上的一个动点，过点Q作y轴的平行线，交直线CF于点D，点E在线段CD的延长线上，连接QE．问：以QD为腰的等腰△QDE的面积是否存在最大值？若存在，请求出这个最大值；若不存在，请说明理由．

    （1）A点坐标为（﹣3，0）；（2）；P点坐标为（， ）；（3）以QD为腰的等腰三角形的面积最大值为． 【解析】试题分析：（1）把B点的坐标代入抛物线的解析式，求出a的值即可，令y=0，解方程求得x的值，即可得点A的坐标；（2）当点P在x轴上方时，连接AP交y轴于点B′，可证△OBP≌△OB′P，可求得B′坐标，利用待定系数法可求得直线AP的解析式，联立直线y=x，可求得P点坐标；当点P在x...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省平凉市中考数学模拟试卷 题型：填空题

    甲、乙两人在相同条件下各射击10次，他们成绩的平均数相同，方差分别是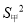=0.2， =0.5，则设两人中成绩更稳定的是_____（填“甲”或“乙”）

    甲 【解析】∵S甲2=0.2，S乙2=0.5， 则S甲2＜S乙2， 可见较稳定的是甲．

    查看答案和解析>>

    科目：初中数学 来源：重庆市校2018届九年级上学期期末模拟数学试卷 题型：解答题

    如图，AB是⊙O的直径，点C，D在圆上，且四边形AOCD是平行四边形，过点D作⊙O的切线，分别交OA的延长线与OC的延长线于点E，F，连接BF.

    （1）求证：BF是⊙O的切线；

    （2）已知圆的半径为1，求EF的长.

    （1）证明见解析；（2）EF=2. 【解析】试题分析：(1)、先证明四边形AOCD是菱形，从而得到∠AOD=∠COD=60°，再根据切线的性质得∠FDO=90°，接着证明△FDO≌△FBO得到∠ODF=∠OBF=90°，然后根据切线的判定定理即可得到结论；(2)、在Rt△OBF中，利用60度的正切的定义求解． 试题解析：(1)、连结OD，如图，∵四边形AOCD是平行四边形，而OA=OC...

    查看答案和解析>>

    同步练习册答案