
关于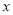 的一元二次方程
的一元二次方程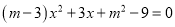 有一个解是
有一个解是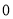 ,则
,则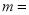 __________.
__________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:单选题
若a+b=3,ab=2,则a2 +b2的值是( )
A. 2.5 B. 5 C. 10 D. 15
B 【解析】试题解析:∵a+b=3,ab=2, ∴a2+b2=(a+b)2-2ab=32-2×2=5. 故选B.查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:填空题
如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则∠AED的余弦值是______.
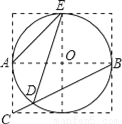
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型:解答题
如图,矩形空地的长为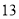 米,宽为
米,宽为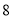 米,计划在其中修建两块相同的矩形绿地,它们的面积之和为
米,计划在其中修建两块相同的矩形绿地,它们的面积之和为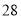 平方米,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米.
平方米,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型:填空题
如图,已知二次函数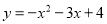 的图象交
的图象交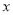 轴于
轴于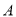 ,
, 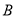 两点(
两点(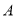 在
在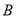 左边),交
左边),交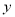 轴于
轴于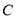 点,点
点,点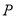 是直线
是直线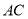 上方抛物线上一动点(不与
上方抛物线上一动点(不与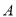 ,
, 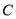 重合),则
重合),则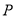 点到直线
点到直线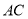 的距离的最大值是__________.
的距离的最大值是__________.
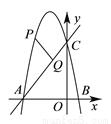
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型:单选题
如图,一次函数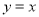 与二次函数
与二次函数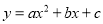 图象相交于
图象相交于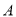 、
、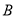 两点,则函数
两点,则函数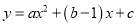 的图象可能是( ).
的图象可能是( ).

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型:单选题
下列方程中是关于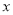 的一元二次方程的是( ).
的一元二次方程的是( ).
A. 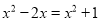 B.
B. 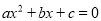
C. 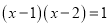 D.
D. 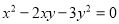
查看答案和解析>>
科目:初中数学 来源:2017年内蒙古乌兰察布市中考数学一模试卷 题型:单选题
已知下列命题:
①若a>0,b>0,则a+b>0;
②若a2=b2,则a=b;
③线段垂直平分线上的点到线段两端点距离相等;
④平行四边形的对角线互相平分
其中原命题与逆命题均为真命题的是( )
A. ①③ B. ②④ C. ③④ D. ②③
C 【解析】试题解析:①若a>0,b>0,则a+b>0,这个命题为真命题,其逆命题为若a+b>0,则a>0,b>0,此逆命题为假命题; ②若,则a=b,这个命题为假命题,其逆命题为若a=b,则,此逆命题为真命题; ③线段垂直平分线上的点到线段两端点距离相等,这个命题为真命题,其逆命题为到线段两端点距离相等的点在线段的垂直平分线上,此逆命题为真命题; ④平行四边形的对角线互相...查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年七年级数学上期末复习检测数学试卷 题型:解答题
如图所示,从一点O出发引射线OA、OB、OC、OD,请你数一数图中有多少个角,并把它们表示出来.
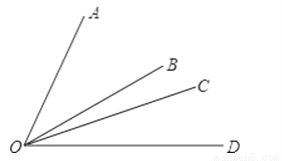
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com