
在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE= ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1)当点P与点C重合时(如图1).求证:△BOG≌△POE;
(2)通过观察、测量、猜想: = ,并结合图2证明你的猜想;
= ,并结合图2证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图3),若∠ACB=α,求 的值.(用含α的式子表示)
的值.(用含α的式子表示)

科目:初中数学 来源:2018年天津市红桥区中考数学模拟试卷(解析) 题型:填空题
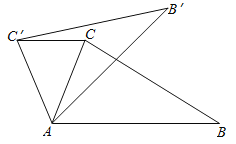
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′= .
查看答案和解析>>
科目:初中数学 来源:沪科版九年级下册数学第26章概率初步单元检测(含答案) 题型:单选题
现有四条线段,长度依次是2,3,4,5,从中任选三条,能组成三角形的概率是( )
A. 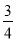 B.
B. 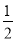 C.
C. 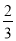 D.
D. 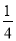
查看答案和解析>>
科目:初中数学 来源:河北省邯郸市2017-2018学年八年级下学期第一次月考数学试卷B4(含答案) 题型:填空题
已知菱形ABCD的两条对角线相交于点O,AC=4,BD=2,则菱形ABCD的周长是___________.
查看答案和解析>>
科目:初中数学 来源:河北省邯郸市2017-2018学年八年级下学期第一次月考数学试卷B4(含答案) 题型:单选题
如图,为测量池塘边A、B两点的距离,小明在池塘的一侧选取一点O,测得OA、OB的中点分别是点D、E,且DE=14m,则A、B间的距离是( )
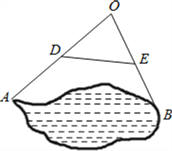
A. 18m B. 24m C. 28m D. 30m
查看答案和解析>>
科目:初中数学 来源:2018年湖北省十堰市丹江口市中考数学模拟试卷(3月份) 题型:解答题
小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离.
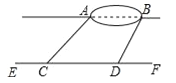
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017-2018学年第二学期八年级期中数学模拟试卷 题型:解答题
如图,四边形ABCD中AB∥CD,对角线AC,BD相交于O,点E,F分别为BD上两点,且BE=DF,∠AEF=∠CFB.
(1)求证:四边形ABCD是平行四边形;
(2)若AC=2OE,试判断四边形AECF的形状,并说明理由.

【答案】(1)(2)见解析
【解析】试题分析:(1)已知AB∥CD,根据两直线平行,内错角相等可得∠ABD=∠CDB,由∠AEF=∠CFB,根据平角的定义可得∠AEB=∠CFD,利用ASA证得△ABE≌△CDF,根据全等三角形的性质可得AB=CD,由AB∥CD,根据一组对边平行且相等的四边形为平行四边形即可得四边形ABCD是平行四边形;(2)平行四边形AECF是矩形,根据平行四边形的性质可得OB=OD ,OA=OC= AC,由BE=DF证得OE=OF,根据对角线互相平分的四边形为平行四边形可判定四边形AECF是平行四边形,再证得AC=EF,根据对角线相等的平行四边形是矩形即可判定平行四边形AECF是矩形.
AC,由BE=DF证得OE=OF,根据对角线互相平分的四边形为平行四边形可判定四边形AECF是平行四边形,再证得AC=EF,根据对角线相等的平行四边形是矩形即可判定平行四边形AECF是矩形.
试题解析:
(1)证明:∵AB∥CD,
∴∠ABD=∠CDB,
又∵∠AEF=∠CFB,
∴∠AEB=∠CFD,
又∵BE=DF,
∴△ABE≌△CDF(ASA),
∴AB=CD,
又∵AB∥CD,
∴四边形ABCD是平行四边形;
(2) 平行四边形AECF是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD ,OA=OC= AC,
AC,
∵BE=DF,
∴OB﹣BE=DO﹣DF,
∴OE=OF,
又∵OA=OC,
∴四边形AECF是平行四边形,
又∵AC=2OE,EF=2OE,
∴AC=EF,
∴平行四边形AECF是矩形.
【题型】解答题
【结束】
23
已知,  ,
, 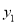 与
与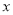 成正比例,
成正比例, 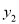 与
与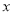 成反比例,并且当
成反比例,并且当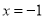 时,
时, 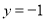 ,当
,当 时,
时, 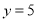 .
.
(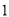 )求
)求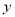 关于
关于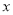 的函数关系式.
的函数关系式.
(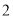 )当
)当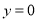 时,求
时,求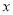 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级下学期第一次月考数学试卷 题型:单选题
下列叙述中,正确的有( )
①如果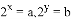 ,那么
,那么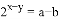 ;②满足条件
;②满足条件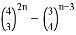 的n不存在;
的n不存在;
③任意一个三角形的三条高所在的直线相交于一点,且这点一定在三角形的内部;
④ΔABC中,若∠A+∠B=2∠C, ∠A-∠C=40°,则这个△ABC为钝角三角形.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com