
如图,四边形ABCD中AB∥CD,对角线AC,BD相交于O,点E,F分别为BD上两点,且BE=DF,∠AEF=∠CFB.
(1)求证:四边形ABCD是平行四边形;
(2)若AC=2OE,试判断四边形AECF的形状,并说明理由.

【答案】(1)(2)见解析
【解析】试题分析:(1)已知AB∥CD,根据两直线平行,内错角相等可得∠ABD=∠CDB,由∠AEF=∠CFB,根据平角的定义可得∠AEB=∠CFD,利用ASA证得△ABE≌△CDF,根据全等三角形的性质可得AB=CD,由AB∥CD,根据一组对边平行且相等的四边形为平行四边形即可得四边形ABCD是平行四边形;(2)平行四边形AECF是矩形,根据平行四边形的性质可得OB=OD ,OA=OC= AC,由BE=DF证得OE=OF,根据对角线互相平分的四边形为平行四边形可判定四边形AECF是平行四边形,再证得AC=EF,根据对角线相等的平行四边形是矩形即可判定平行四边形AECF是矩形.
AC,由BE=DF证得OE=OF,根据对角线互相平分的四边形为平行四边形可判定四边形AECF是平行四边形,再证得AC=EF,根据对角线相等的平行四边形是矩形即可判定平行四边形AECF是矩形.
试题解析:
(1)证明:∵AB∥CD,
∴∠ABD=∠CDB,
又∵∠AEF=∠CFB,
∴∠AEB=∠CFD,
又∵BE=DF,
∴△ABE≌△CDF(ASA),
∴AB=CD,
又∵AB∥CD,
∴四边形ABCD是平行四边形;
(2) 平行四边形AECF是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD ,OA=OC= AC,
AC,
∵BE=DF,
∴OB﹣BE=DO﹣DF,
∴OE=OF,
又∵OA=OC,
∴四边形AECF是平行四边形,
又∵AC=2OE,EF=2OE,
∴AC=EF,
∴平行四边形AECF是矩形.
【题型】解答题
【结束】
23
已知,  ,
, 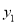 与
与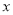 成正比例,
成正比例, 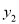 与
与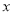 成反比例,并且当
成反比例,并且当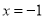 时,
时, 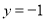 ,当
,当 时,
时, 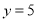 .
.
(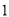 )求
)求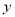 关于
关于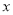 的函数关系式.
的函数关系式.
(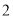 )当
)当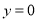 时,求
时,求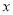 的值.
的值.
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源:沪科版九年级下册数学第26章概率初步单元检测(含答案) 题型:填空题
小明在做掷一枚普通的正方体骰子实验,请写出这个实验中一个可能发生的事件:________
查看答案和解析>>
科目:初中数学 来源:2018年湖北省十堰市丹江口市中考数学模拟试卷(3月份) 题型:解答题
在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE= ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1)当点P与点C重合时(如图1).求证:△BOG≌△POE;
(2)通过观察、测量、猜想: = ,并结合图2证明你的猜想;
= ,并结合图2证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图3),若∠ACB=α,求 的值.(用含α的式子表示)
的值.(用含α的式子表示)

查看答案和解析>>
科目:初中数学 来源:2018年湖北省十堰市丹江口市中考数学模拟试卷(3月份) 题型:单选题
有两块面积相同的小麦试验田,分别收获小麦9000kg和15000kg.已知第一块试验田每公顷的产量比第二块少3000kg,若设第一块试验田每公顷的产量为x kg,由题意可列方程( )
A. 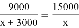 B.
B. 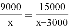 C.
C. 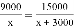 D.
D. 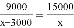
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017-2018学年第二学期八年级期中数学模拟试卷 题型:解答题
如图,E为正方形ABCD对角线BD上的一点,且BE=BC=1.

(1)求∠DCE的度数;
(2)点P在EC上,作PM⊥BD于M,PN⊥BC于N,求PM+PN的值.
【答案】(1)22.5°,(2)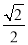 .
.
【解析】
试题分析:(1)由正方形的性质得到,∠BCD=90°,∠DBC=45°,推出AB=BE,根据三角形的内角和定理求出∠BCE=∠BEC=67.5°,根据∠DCE=∠DCB-∠BCE即可求出答案.
(2)连接BP,作EF⊥BC于F,则∠EFB=90°,得出△BEF是等腰直角三角形,从而求得BF=EF=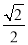 ,然后根据S△BPE+S△BPC=S△BEC,求得PM+PN=EF,即可求得.
,然后根据S△BPE+S△BPC=S△BEC,求得PM+PN=EF,即可求得.
试题解析:(1)在正方形ABCD中,∠BCD=90°,∠DBC=45°,
∵BE=BC,
∴AB=BE,
∴∠BCE=∠BEC=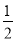 (180°-∠DBC)=67.5°,
(180°-∠DBC)=67.5°,
∴∠DCE=∠DCB-∠BCE=90°-67.5°=22.5°,
(2)连接BP,作EF⊥BC于F,则∠EFB=90°,
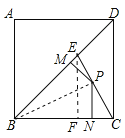
∵∠EBF=45°,
∴△BEF是等腰直角三角形,
∵BE=BC=1,
∴BF=EF=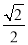 ,
,
∵PM⊥BD,PN⊥BC,
∴S△BPE+S△BPC=S△BEC,
即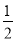 BE•PM+
BE•PM+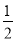 BC•PN=
BC•PN=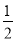 BC•EF,
BC•EF,
∵BE=BC,
∴PM+PN=EF=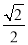 .
.
考点:1.正方形的性质;2.等腰直角三角形.
【题型】解答题
【结束】
28
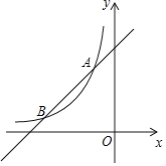
如图,一次函数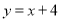 的图像与反比例函数
的图像与反比例函数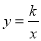 (
(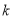 为常数,且
为常数,且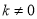 )的图像交于
)的图像交于
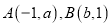 两点.
两点.
(1)求反比例函数的表达式;
(2)在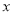 轴上找一点
轴上找一点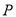 ,使
,使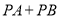 的值最小,求满足条件的点
的值最小,求满足条件的点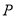 的坐标;
的坐标;
(3)在(2)的条件下求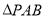 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017-2018学年第二学期八年级期中数学模拟试卷 题型:填空题
反比例函数y= 的图象经过点(1,6)和(m,-3),则m= .
的图象经过点(1,6)和(m,-3),则m= .
【答案】-2.
【解析】
试题分析:先把点(1,6)代入反比例函数y= ,求出k的值,进而可得出反比例函数的解析式,再把点(m,-3)代入即可得出m的值.
,求出k的值,进而可得出反比例函数的解析式,再把点(m,-3)代入即可得出m的值.
试题解析:∵反比例函数y= 的图象经过点(1,6),
的图象经过点(1,6),
∴6= ,解得k=6,
,解得k=6,
∴反比例函数的解析式为y= .
.
∵点(m,-3)在此函数图象上,
∴-3= ,解得m=-2.
,解得m=-2.
考点:反比例函数图象上点的坐标特征.
【题型】填空题
【结束】
18
如图,已知点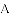
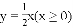 图像上一点,过点
图像上一点,过点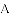
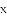
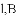

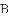
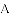


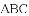
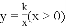 的图像过点
的图像过点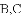
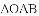
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017-2018学年第二学期八年级期中数学模拟试卷 题型:填空题
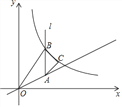
如图所示,在RT△AO中, 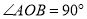 ,
, 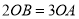 ,点
,点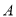 在反比例函数
在反比例函数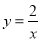 的图像上,若点
的图像上,若点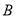 在反比例函数
在反比例函数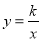 的图像上,则
的图像上,则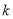 的值为( ).
的值为( ).
A.  B.
B.  C.
C. 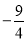 D.
D. 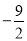
【答案】D
【解析】过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D.
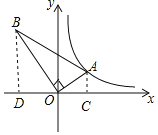
设点A的坐标是(m,n),则AC=n,OC=m,
∵∠AOB=90°,∴∠AOC+∠BOD=90°,
∵∠DBO+∠BOD=90°,∴∠DBO=∠AOC,
∵∠BDO=∠ACO=90°,∴△BDO∽△OCA,∴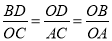 ,
,
∵2OB=3OA,∴BD=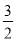 m,OD=
m,OD=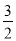 n,
n,
因为点A在反比例函数y=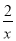 的图象上,则mn=2,
的图象上,则mn=2,
∵点B在反比例函数y=kx的图象上,B点的坐标是(?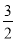 n ,
n , 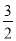 m),
m),
∴k=?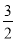 n?
n?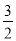 m=?
m=?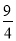 mn=?
mn=?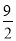 .
.
故选D.
【题型】单选题
【结束】
11
在函数y=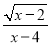 中,自变量x的取值范围是______.
中,自变量x的取值范围是______.
查看答案和解析>>
科目:初中数学 来源:青岛版九年级下册数学 第6章事件的概率 单元检测 题型:单选题
小明、小雪、丁丁和东东在公园玩飞行棋,四人轮流掷骰子,小明掷骰子7次就掷出了4次6,则小明掷到数字6的概率是( )
A.  B.
B.  C.
C.  D. 不能确定
D. 不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com