
如图,为测量池塘边A、B两点的距离,小明在池塘的一侧选取一点O,测得OA、OB的中点分别是点D、E,且DE=14m,则A、B间的距离是( )
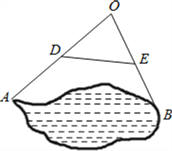
A. 18m B. 24m C. 28m D. 30m
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源:2018年天津市红桥区中考数学模拟试卷(解析) 题型:解答题
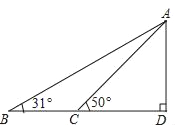
如图,在一条笔直公路BD的正上方A处有一探测仪,AD=24m,∠D=90°,一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.
(Ⅰ)求B,C两点间的距离(结果精确到1m);
(Ⅱ)若规定该路段的速度不得超过15m/s,判断此轿车是否超速.
参考数据:tan31°≈0.6,tan50°≈1.2.
查看答案和解析>>
科目:初中数学 来源:沪科版九年级下册数学第26章概率初步单元检测(含答案) 题型:单选题
某十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时,是黄灯的概率为( )
A. 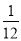 B.
B. 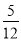 C.
C. 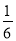 D.
D. 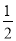
查看答案和解析>>
科目:初中数学 来源:河北省邯郸市2017-2018学年八年级下学期第一次月考数学试卷B4(含答案) 题型:填空题
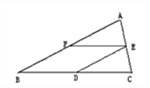
如图,在△ABC中,AB=BC,D、E、F分别是BC、AC、AB边上的中点.若AB=12cm,则四边形BDEF的周长为___________.
查看答案和解析>>
科目:初中数学 来源:河北省邯郸市2017-2018学年八年级下学期第一次月考数学试卷B4(含答案) 题型:单选题
如图,已知△ABC的面积为36,将△ABC沿BC平移到△A’B’C’,使B’和C重合,连结AC’交AC于D,则△C’AC的面积为( )
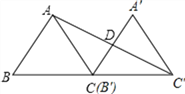
A. 36 B. 18 C. 12 D. 9
查看答案和解析>>
科目:初中数学 来源:2018年湖北省十堰市丹江口市中考数学模拟试卷(3月份) 题型:解答题
在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE= ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1)当点P与点C重合时(如图1).求证:△BOG≌△POE;
(2)通过观察、测量、猜想: = ,并结合图2证明你的猜想;
= ,并结合图2证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图3),若∠ACB=α,求 的值.(用含α的式子表示)
的值.(用含α的式子表示)

查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017-2018学年第二学期八年级期中数学模拟试卷 题型:解答题
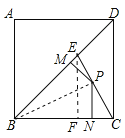
如图,E为正方形ABCD对角线BD上的一点,且BE=BC=1.

(1)求∠DCE的度数;
(2)点P在EC上,作PM⊥BD于M,PN⊥BC于N,求PM+PN的值.
【答案】(1)22.5°,(2)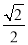 .
.
【解析】
试题分析:(1)由正方形的性质得到,∠BCD=90°,∠DBC=45°,推出AB=BE,根据三角形的内角和定理求出∠BCE=∠BEC=67.5°,根据∠DCE=∠DCB-∠BCE即可求出答案.
(2)连接BP,作EF⊥BC于F,则∠EFB=90°,得出△BEF是等腰直角三角形,从而求得BF=EF=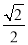 ,然后根据S△BPE+S△BPC=S△BEC,求得PM+PN=EF,即可求得.
,然后根据S△BPE+S△BPC=S△BEC,求得PM+PN=EF,即可求得.
试题解析:(1)在正方形ABCD中,∠BCD=90°,∠DBC=45°,
∵BE=BC,
∴AB=BE,
∴∠BCE=∠BEC=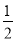 (180°-∠DBC)=67.5°,
(180°-∠DBC)=67.5°,
∴∠DCE=∠DCB-∠BCE=90°-67.5°=22.5°,
(2)连接BP,作EF⊥BC于F,则∠EFB=90°,
∵∠EBF=45°,
∴△BEF是等腰直角三角形,
∵BE=BC=1,
∴BF=EF=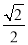 ,
,
∵PM⊥BD,PN⊥BC,
∴S△BPE+S△BPC=S△BEC,
即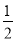 BE•PM+
BE•PM+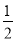 BC•PN=
BC•PN=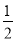 BC•EF,
BC•EF,
∵BE=BC,
∴PM+PN=EF=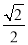 .
.
考点:1.正方形的性质;2.等腰直角三角形.
【题型】解答题
【结束】
28
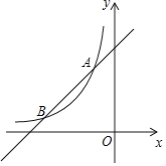
如图,一次函数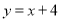 的图像与反比例函数
的图像与反比例函数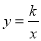 (
(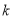 为常数,且
为常数,且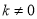 )的图像交于
)的图像交于
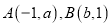 两点.
两点.
(1)求反比例函数的表达式;
(2)在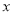 轴上找一点
轴上找一点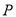 ,使
,使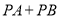 的值最小,求满足条件的点
的值最小,求满足条件的点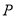 的坐标;
的坐标;
(3)在(2)的条件下求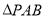 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级下学期第一次月考数学试卷 题型:填空题
在等腰△ABC中,如果两边长分别为6cm、10cm,则这个等腰三角形的底边长为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com