
����μ����е���̨��֯�ġ�ĵ���������������Ŀ��������������ѡ���˳��ͨ�أ���һ����ѡ����3��ѡ��ڶ�����ѡ����4��ѡ��������������ᣬ����������������������������(ʹ�á�������һ�ο�����������ȥ������һ���һ������ѡ��)��
(1)����������Ρ����������ڵ�һ������ʹ�ã���ô����ͨ�صĸ�����________��
(2)����������Ρ����������ڵڶ�������ʹ�ã���ô����ͨ�صĸ�����________��
(3)�������ÿ�������һ�Ρ���������������״ͼ�����б���������˳��ͨ�صĸ��ʣ�
��1����2����3�� �������������������1���������Ρ����������ڵ�һ������ʹ�ã���һ���϶��ܶԣ��ڶ����Եĸ���Ϊ�����ɵó������ ��2��������ó���һ����Եĸ���Ϊ���ڶ�����Եĸ���Ϊ�����ɵó������ ��3������״ͼ�ó�����6�ֵȿ��ܵĽ��������˳��ͨ�ص�ֻ��1����������ɵó������ �����������1����һ���϶��ܶԣ��ڶ����Եĸ���Ϊ�� ��������ͨ�صĸ���Ϊ�� ��... �żӾ���ϵ�д�
�żӾ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�Ƹ���2017-2018ѧ����꼶���ϣ�������ѧ�� ���ͣ������
��ͼ,��������������,��������С�������α�Ϳ��,�ٽ�ͼ������С��������Ϳ��һ��,ʹ������Ϳ�ڵ�ͼ������һ����Գ�ͼ�εķ�����______��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ�����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
��ͼ��ֱ��l����AB���㣬AB��18cm����O���߶�AB�ϵ�һ�㣬OA��2OB

��1��OA�� cm �� OB�� cm��
��2������C��ֱ��AB��һ�㣬������AC��CO+CB����CO�ij���
��3��������P��Q�ֱ��A��Bͬʱ�����������˶�����P���ٶ�Ϊ2cm/s����Q���ٶ�Ϊ1cm/s�����˶�ʱ��Ϊts������P���Q�غ�ʱ��P��Q����ֹͣ�˶���
�ٵ�tΪ��ֵʱ��2OP��OQ��3��
�ڵ���P������Oʱ������M�ӵ�O��������4cm/s���ٶ�Ҳ�����˶�������M�ϵ�Q���������أ���4cm/s���ٶ����P�˶���������P�����������أ���4cm/s���ٶ����Q�˶����������.����P���Q�غ�ʱ��P��Q����ֹͣ�˶�����ʱ��MҲֹͣ�˶����ڴ˹����У���M��ʻ����·���Ƕ��٣�
��1��12��6����2��CO�ij�Ϊ2��18cm����3���ٵ�tΪ3s��11sʱ��2OP��OQ=3���� 48cm�� ���������������: ��1����OA=2OB���AB=OA+OB=18�������OA��OB�ij��ȣ� ��2����CO�ij���xcm���ֵ�C���߶�AO�ϡ����߶�OB���Լ����߶�AB���ӳ���������������ǣ����������ľ��빫ʽ���AC=CO+CB���ɵó�����x��һԪһ�η��̣���֮���ɵó����ۣ�...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ�����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
��4a��2b��1����3+8a��4b��_____��
5 ����������4a?2b=1�� ��3+8a?4b=3+2(4a?2b)=3+2=5. �ʴ�Ϊ��5.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ�����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ���ѡ��
��֪̫���İ뾶ԼΪ696000000m����696000000������ÿ�ѧ�������ɱ�ʾΪ �� ��.
A. 0��696��109 B. 6��96��109
C. 6��96��108 D. 69��6��107
C ��������������������ݿ�ѧ�������Ķ��壬696 000 000=6��96��108. ��ѡ��C.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��֪����x�Ķ��κ���y=ax2+��a2��1��x��a��ͼ����x���һ�����������Ϊ��m��0������3��m��4����a��ȡֵ��Χ��_____��
��a����4��a����3 ����������y=ax2+��a2��1��x��a=��ax��1����x+a���� �൱y=0ʱ���ɽ�ã�x1=��x2=��a�� ����������x��Ľ���Ϊ����0���ͣ���a��0���� ����������x���һ�����������Ϊ��m��0����2��m��3�� �ࣨ1����a��0ʱ��3����4����ã� ��2����a��0ʱ��3����a��4����é�4��a����3�� ����������a��ȡֵ��Χ��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
��ͼ����ֽ�ϼ���һ��Բ�κ�һ�����ε�ֽƬ��ʹ֮ǡ����Χ��һ��Բģ�ͣ���Բ�İ뾶Ϊr�����εİ뾶ΪR�����ε�Բ�Ľǵ���90�㣬��r��R֮��Ĺ�ϵ��( )
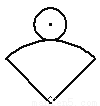
A. R��2r�� B. 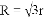 �� C. R��3r�� D. R��4r��
�� C. R��3r�� D. R��4r��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������ɳ�ӿ�����ҹ�������ѧУ2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
һ����λ������λ���ֱ�ʮλ���ִ�3����λ���ֵ�ƽ���պõ��������λ�����������λ����________��
25��36 �������������������ʮλ����Ϊx���λ����Ϊx+3,������λ��Ϊ10x+x+3 = 11x+3����Ϊ��λ���ֵ�ƽ���պõ��������λ��������= 11x+3�����x= 2��3,���Եõ�25,��36���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ� ��ʮ���� ��Գ� 13.1 ��Գ� ͬ����ϰ�� ���ͣ������
��ͼ��ʾ,�ڡ�ABC��,��ACB=90��,D��AB��һ��,��BD=BC,��D��AB�Ĵ��߽�AC�ڵ�E,����CD,BE���ڵ�F.��֤:BE��CD�Ĵ�ֱƽ����.
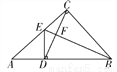
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com