
方程组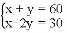 的解是( )
的解是( )
A. 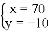 B.
B. 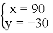 C.
C. 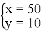 D.
D. 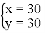
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:单选题
如图,在△ABC中,∠C=90°,AC=3,BC=4,将△ABC绕点A逆时针旋转,使点C落在线段AB上点E处,点B落在点D处,则线段BE的长度为 ( )
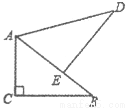
A. 2 B. 3 C. 4 D. 2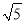
查看答案和解析>>
科目:初中数学 来源:江苏省徐州市区联校2017-2018学年八年级上学期期中联考数学试卷 题型:单选题
下列性质中,等腰三角形具有而直角三角形不一定具有的是( )
A.任意两边之和大于第三边
B.内角和等于180°
C.有两个锐角的和等于90°
D.有一个角的平分线垂直于这个角的对边
D 【解析】 试题分析:根据等腰三角形与直角三角形的性质作答. 【解析】 A、对于任意一个三角形都有两边之和大于第三边,不符合题意; B、对于任意一个三角形都有内角和等于180°,不符合题意; C、只有直角三角形才有两个锐角的和等于90°,不符合题意; D、等腰三角形顶角的平分线垂直于顶角的对边,而直角三角形(等腰直角三角形除外)没有任何一个角的平分线垂直于这...查看答案和解析>>
科目:初中数学 来源:湖南省新化县2016-2017学年度第二学期期中检测七年级数学试卷 题型:填空题
多项式(x-m)(x-n)的展开结果中x的一次项系数为3,常数项为2,则m2n+mn2的值为 ________.
-6 【解析】【解析】 ∵(x-m)(x-n)=x2-(m+n)x+mn,∴m+n=-3,mn=2,∴m2n+mn2=mn(m+n)=2×(-3)=-6.故答案为:-6.查看答案和解析>>
科目:初中数学 来源:湖南省新化县2016-2017学年度第二学期期中检测七年级数学试卷 题型:单选题
当a=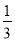 时,代数式(a-4)(a-3)-a(a+2)的值为( )
时,代数式(a-4)(a-3)-a(a+2)的值为( )
A. 9 B. -9 C. 3 D. 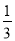
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
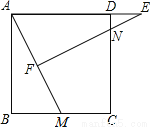
如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:填空题
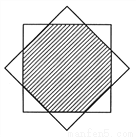
如图,将边长为(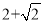 )cm的正方形绕其中心旋转45°,则两个正方形公共部分(图中阴影部分)的面积为___________cm2.
)cm的正方形绕其中心旋转45°,则两个正方形公共部分(图中阴影部分)的面积为___________cm2.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:单选题
抛物线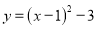 的对称轴是( )
的对称轴是( )
A. y轴 B. 直线x=﹣3 C. 直线x=﹣1 D. 直线x=1
D 【解析】抛物线y=(x-1)2-3是抛物线的顶点式, 根据抛物线的顶点式可知抛物线y=(x-1)2-3的对称轴是直线x=1. 故选C.查看答案和解析>>
科目:初中数学 来源:2017年河南省中考数学三模试卷 题型:填空题
已知函数y=(k﹣3)x2+2x+1的图象与x轴有交点,则k的取值范围是( )
A. k<4 B. k≤4 C. k<4且k≠3 D. k≤4且k≠3
B 【解析】试题分析:(1)当k-3=0,即k=3时,函数y=2x+1的图象与x轴有交点;(2)当时,二次函数y=(k-3)x2+2x+1的图象与x轴有交点,则,所以k≤4,所以k≤4且k≠3,由(1)(2)可知,当k≤4时,函数y=(k-3)x2+2x+1的图象与x轴有交点,故选:B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com