
���������У����������ξ��ж�ֱ�������β�һ�����е��ǣ� ��
A.��������֮�ʹ��ڵ�����
B.�ڽǺ͵���180��
C.��������ǵĺ͵���90��
D.��һ���ǵ�ƽ���ߴ�ֱ������ǵĶԱ�
D �������� ������������ݵ�����������ֱ�������ε��������� �������� A����������һ�������ζ�������֮�ʹ��ڵ����ߣ����������⣻ B����������һ�������ζ����ڽǺ͵���180�㣬���������⣻ C��ֻ��ֱ�������β���������ǵĺ͵���90�㣬���������⣻ D�����������ζ��ǵ�ƽ���ߴ�ֱ�ڶ��ǵĶԱߣ���ֱ�������Σ�����ֱ�������γ��⣩û���κ�һ���ǵ�ƽ���ߴ�ֱ����... �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㽭ʡ����2017-2018ѧ����꼶�ϲ���ĩģ����ѧ�Ծ� ���ͣ���ѡ��
�ܰ������ε����ƽ�ֵ��� �� ��
A. �����εĽ�ƽ���� B. �����εĸ� C. �����ε����� D. ���϶�����
C �����������������������֪�����������Ϊ����֮һ�ߵij˻�������ѡ���У�ֻ�������ܹ�ƽ�ֵױߣ�ʹ������ƽ��Ϊ���������ȵ�С�����Ρ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʮһ���п���ѧ����Ծ���һ�� ���ͣ���ѡ��
��ͼ��������ABCD�ı߳�Ϊ4����P��Q�ֱ���CD��AD���е㣬����E�ӵ�A���B�˶�������Bʱֹͣ�˶���ͬʱ������F�ӵ�P��������P��D��Q�˶�����E��F���˶��ٶ���ͬ�����E���˶�·��Ϊx����AEF�����Ϊy���ܴ��¿̻�y��x�ĺ�����ϵ��ͼ���ǣ�������
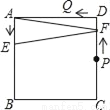
A. 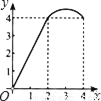 B.
B. 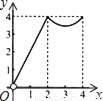 C.
C. 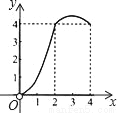 D.
D. 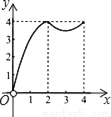
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ����������У2017-2018ѧ����꼶��ѧ������������ѧ�Ծ� ���ͣ������
��֪����ͼ���ڡ�ABC�У�AB=AC����D��E�ֱ���AB��AC�ϣ���DE��BC����֤��AD=AE��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ����������У2017-2018ѧ����꼶��ѧ������������ѧ�Ծ� ���ͣ������
��ͼ�����ı���ABCD�У�AD=AB����B=��D=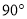 ����ACB=
����ACB=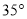 �����DAB=_____�㣮
�����DAB=_____�㣮
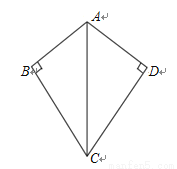
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ����������У2017-2018ѧ����꼶��ѧ������������ѧ�Ծ� ���ͣ���ѡ��
����ͼ���У�������Գ�ͼ�ε���( )
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�»���2016-2017ѧ��ȵڶ�ѧ�����м�����꼶��ѧ�Ծ� ���ͣ������
�����з����飺
(1)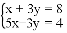
(2)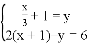
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�»���2016-2017ѧ��ȵڶ�ѧ�����м�����꼶��ѧ�Ծ� ���ͣ���ѡ��
������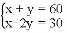 �Ľ���( )
�Ľ���( )
A. 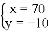 B.
B. 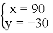 C.
C. 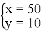 D.
D. 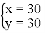
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ̩����2017���п���ѧ��ģ�Ծ��������棩 ���ͣ������
�㣨a��1��y1������a+1��y2���ڷ���������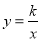 ��k��0����ͼ���ϣ���y1��y2����a�ķ�Χ�� ��
��k��0����ͼ���ϣ���y1��y2����a�ķ�Χ�� ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com