
下列图形中不是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
科目:初中数学 来源:山东省2017-2018学年七年级上期末复习检测数学试卷 题型:解答题
比-1小的整数如下列这样排列
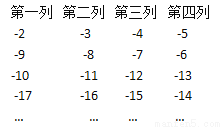
在上述的这些数中,观察它们的规律,回答数-100将在哪一列.
第三列. 【解析】试题分析:观察图形可知,8个数字一个循环周期,-2到-100一共有100-2+1=99个数字,99÷8=12…3,所以-100是第13循环周期的第3个数字,所以在第三列,据此即可解答问题. 试题解析:因为-2到-100一共有100-2+1=99个数字, 99÷8=12…3, 所以-100是第13循环周期的第3个数字,所以在第三列, 答:-100在第三...查看答案和解析>>
科目:初中数学 来源:重庆市江北区2018届九年级上期末模拟数学试卷 题型:单选题
某县大力推进义务教育均衡发展,加强学校标准化建设,计划用三年时间对全县学校的设施和设备进行全面改造,2014年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2016年投资7.2亿元人民币,那么每年投资的增长率为( )
A. 20% B. 40% C. -220% D. 30%
A 【解析】试题分析:首先设每年投资的增长率为x.根据2014年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2016年投资7.2亿元人民币,列方程求解. 【解析】 设每年投资的增长率为x, 根据题意,得:5(1+x)2=7.2, 解得:x1=0.2=20%,x2=﹣2.2(舍去), 故每年投资的增长率为为20%. 故选:A.查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(三) 题型:填空题
如图,将三角板的直角顶点放在直尺的一边上,若∠1=55°,则∠2的度数为_______°.
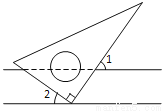
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(三) 题型:单选题
某服装加工厂计划加工400套运动服,在加工完160套后,采用了新技术,工作效率比原计划提高了20%,结果共用了18天完成全部任务.设原计划每天加工x套运动服,根据题意可列方程为( )
A. 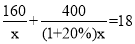 B.
B. 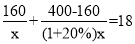
C. 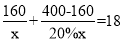 D.
D. 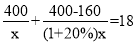
查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市资兴市兴华实验学校中考数学模拟试卷 题型:解答题
如图1,延长⊙O的直径AB至点C,使得BC=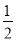 AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.
AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.
(1)∠C的最大度数为 ;
(2)当⊙O的半径为3时,△OPC的面积有没有最大值?若有,说明原因并求出最大值;若没有,请说明理由;
(3)如图2,延长PO交⊙O于点D,连结DB,当CP=DB时,求证:CP是⊙O的切线.
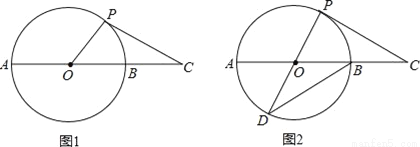
查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市资兴市兴华实验学校中考数学模拟试卷 题型:填空题
观察下列数据:﹣2, 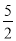 ,
, 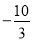 ,
, 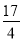 ,﹣
,﹣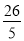 ,…,它们是按一定规律排列的,依照此规律,第11个数据是_____.
,…,它们是按一定规律排列的,依照此规律,第11个数据是_____.
查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:解答题
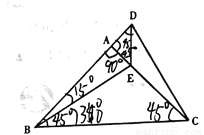
如图,在△ABC中.AB=AC.∠BAC=90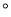 .E是AC边上的一点,延长BA至D,使AD=AE,连接DE,CD.
.E是AC边上的一点,延长BA至D,使AD=AE,连接DE,CD.
(l)图中是否存在两个三角形全等?如果存在请写出哪两个三角形全等,并且证明;如果不存在,请说明理由;
(2)若∠CBE=30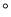 ,求∠ADC的度数.
,求∠ADC的度数.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:填空题
如图,平面上两个正方形与正五边形都有一条公共边,则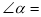 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com