
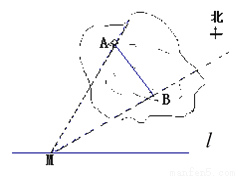
С����֪����������СͤA��B֮��ľ��룬������СͤA��Bλ��ͬһˮƽ���Ҷ�������ĺ���С�� ��ijһ�۲��M�������ͤA�ڵ�M�ı�ƫ��30�㷽��, ͤB�ڵ�M�ı�ƫ��60�㷽��,��С���ɵ�M��С��
��ijһ�۲��M�������ͤA�ڵ�M�ı�ƫ��30�㷽��, ͤB�ڵ�M�ı�ƫ��60�㷽��,��С���ɵ�M��С�� ����60��ʱ�������N������ʱ���ͤAǡ��λ�ڵ�N����������������30��ʱ�����Q������ʱͤBǡ��λ�ڵ�Q���������������ϲ������ݣ��������С�������������СͤA��B֮��ľ��룮
����60��ʱ�������N������ʱ���ͤAǡ��λ�ڵ�N����������������30��ʱ�����Q������ʱͤBǡ��λ�ڵ�Q���������������ϲ������ݣ��������С�������������СͤA��B֮��ľ��룮
 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д� �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ��̨�е�����������2017-2018ѧ��ȵ�һѧ�ڵ����νμ�����꼶��ѧ�Ծ� ���ͣ������
��ͼ��������A��B�����Ӧ���������ֱ�Ϊ10��15����P�ӵ�A��������ÿ��1����λ���ȵ��ٶ��������������˶�����Qͬʱ��ԭ��O��������ÿ��2����λ���ȵ��ٶ��������������˶������˶�ʱ��Ϊt�룮

(1)��0��t��5ʱ���ú�t��ʽ����գ�
BP��_______��AQ��_______��
(2)��t��2ʱ����PQ��ֵ��
(3)��PQ��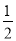 ABʱ����t��ֵ��
ABʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧ��ģ�Ծ� ���ͣ���ѡ��
��֪����������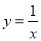 �����н����в���ȷ���ǣ� ��
�����н����в���ȷ���ǣ� ��
A. ͼ���㣨��1����1�� B. ͼ���ڵ�һ��������
C. ��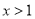 ʱ��
ʱ�� 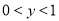 D. ��
D. ��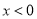 ʱ��y����x�����������
ʱ��y����x�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ �������� ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У���֪�ı���ABCDΪ���Σ���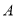 ��0��3����
��0��3����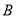 ����4��0����
����4��0����
��1������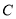 �ķ����������Ľ���ʽ��
�ķ����������Ľ���ʽ��
��2����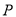 �ǣ�1����������ͼ����һ�㣬��
�ǣ�1����������ͼ����һ�㣬��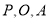 ����������ε�������COD�������ȣ����P�����꣮
����������ε�������COD�������ȣ����P�����꣮
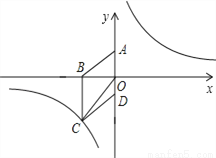
���𰸡���1��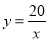 ����2��P��
����2��P��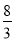 ��
�� 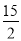 ����-
����-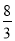 ��-
��-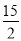 ����
����
������������������ۺϿ��鷴�������������ε����ʣ�ע�⣺�������ε����ʵõ���C�����ꣻ��P�ĺ���������������.
��1���������ε����ʿɵ����εı߳��������ɵõ�C�����꣬���뷴������������ʽ�ɵ�����Ľ���ʽ�� ��2�������P�����꣬�á�COD����������õ�P�ĺ������ʾ����PAO���������ô�ɵõ�P�ĺ����꣬������˵�P������.
�����������1��������֪��OA=3��OB=4��
��Rt��AOB��AB=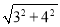 =5��
=5��
���ı���ABCDΪ���Σ�
��AD=BC=AB=5��
��C��-4��-5����
�辭����C�ķ����������Ľ���ʽΪy=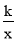 ��k��0����
��k��0����
��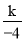 =-5�����k=20��
=-5�����k=20��
������ķ����������Ľ���ʽΪy=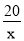 ��
��
��2����P��x��y����
��AD=AB=5��OA=3��
��OD=2��S��COD=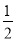 ��2��4=4��
��2��4=4��
��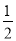 •OA•|x|=4��
•OA•|x|=4��
��|x|=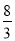 ��
��
��x=��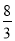 ����
����
��x=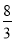 ʱ��y=
ʱ��y=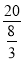 =
=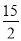 ����x=-
����x=-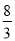 ʱ��y=
ʱ��y=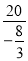 =-
=-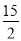 ��
��
��P��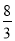 ��
�� 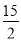 ����?
����?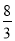 ��?
��?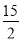 ����
����
���㣺�����������ۺ��⣮
�����͡������
��������
14
��ͼ����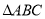 �У�
�� 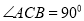 ����
����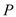 ��
��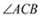 ���ߵľ�����ȣ���
���ߵľ�����ȣ��� ��
��
��1�����ó߹���������Ҫ��ĵ�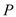 ��������ͼ�ۼ�������Ҫд��������Ȼ���жϡ�ABP����״����˵�����ɣ�
��������ͼ�ۼ�������Ҫд��������Ȼ���жϡ�ABP����״����˵�����ɣ�
��2����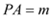 ��
��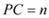 ������
������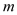 ��
��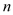 �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ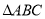 ���ܳ��������
���ܳ��������
��3���� ��
��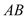 ���ڵ�
���ڵ�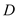 ����̽������
����̽������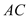 ��
��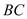 �ij��ȱ仯ʱ��
�ij��ȱ仯ʱ��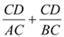 ��ֵ�Ƿ����仯�������䣬�������������ֵ�����仯����˵�����ɣ�
��ֵ�Ƿ����仯�������䣬�������������ֵ�����仯����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ �������� ���ͣ������
��ͼ����������������϶��ɵ�һ������ͼ�ε�����ͼ������ͼ������ߴ磨��λ��mm�������������ͼ�εı������

���𰸡�200mm2.
�������������������������ͼ��֪����ͼ������ij�����ij��������߷ֱ�Ϊ8mm��6mm��2mm������ij�����ij��������߷ֱ�Ϊ4mm��2mm��4mm.�ɴ˼����������ͼ�εı��������.
���������
��������ͼ��֪����ͼ������ij�����ij��������߷ֱ�Ϊ8mm��6mm��2mm������ij�����ij��������߷ֱ�Ϊ4mm��2mm��4mm.
���������ͼ�εı����Ϊ��2(8��6��6��2��8��2)��2(4��2��2��4��4��4)��2��4��2��200(mm2)��
���������ͼ�εı����Ϊ200mm2.
�����͡������
��������
7
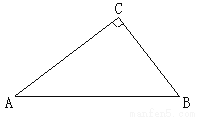
��ͼ��ij��վ���ͻ����ƽ��ʾ��ͼ. Ϊ����ߴ����̵İ�ȫ�ԣ�����ʦ������С���ʹ������ļнǣ�ʹ����45���Ϊ30��. ��֪ԭ���ʹ�AB��Ϊ4��.
��1�����´��ʹ�AC�ij��ȣ�
��2�������Ҫ�ڻ����ŵص�C���������2��ͨ�������жϾ���B��4�Ļ��� �Ƿ���ҪŲ�ߣ���˵�����ɣ�
�Ƿ���ҪŲ�ߣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ������
����֪��������ѭ��С��������ת��Ϊ���������磺��0. 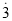 ת��Ϊ����ʱ������0.
ת��Ϊ����ʱ������0. 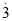 =
= 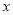 ����
����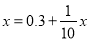 �����
�����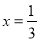 ����0.
����0. 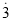 =
=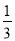 ���´˷�������0.
���´˷�������0. 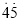 ���ɷ�����_______.
���ɷ�����_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ������
��a��b��Ϊ�෴��,c��d��Ϊ����,�Om�O=2�� 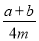 +m2��3cd=___________
+m2��3cd=___________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ���ѡ��
��ij�ֱ��Ѷ���ʽ���з���ʱ��3x3��4��a2b+ab2+1����ͬһ�࣬��������һ������ʽҲ���ڴ��ࣨ������
A. abc��1 B. x2��2 C. 3x2+2xy4 D. m2+2mn+n2
A ���������Ӷ���ʽ�Ĵ���������⣮ �������� 3x3��4��a2b+ab2+1����ͬһ�࣬����3�ζ���ʽ�� A��abc��1��3�ζ���ʽ���ʱ�ѡ����ȷ�� B��x2��2��2�ζ���ʽ���ʱ�ѡ����� C��3x2+2xy4��5�ζ���ʽ���ʱ�ѡ����� D��m2+2mn+n2��2�ζ���ʽ���ʱ�ѡ����� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶��ʦ�����ѧ�Ծ���B���� ���ͣ������
��֪��A��2a+3b��-2����A����-1��3a+b������y��Գƣ���a+b��ֵΪ_______.
0 ������������������ߵ�A��2a+3b��-2���͵�A�䣨-1��3a+b������y��Գƣ� ��2a+3b=1��3a+b=-2�� ��2��2a+3b��+3a+b=1��2+��-2��=0�� ��a+b=0.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com