
��ͼ����������������϶��ɵ�һ������ͼ�ε�����ͼ������ͼ������ߴ磨��λ��mm�������������ͼ�εı������

���𰸡�200mm2.
�������������������������ͼ��֪����ͼ������ij�����ij��������߷ֱ�Ϊ8mm��6mm��2mm������ij�����ij��������߷ֱ�Ϊ4mm��2mm��4mm.�ɴ˼����������ͼ�εı��������.
���������
��������ͼ��֪����ͼ������ij�����ij��������߷ֱ�Ϊ8mm��6mm��2mm������ij�����ij��������߷ֱ�Ϊ4mm��2mm��4mm.
���������ͼ�εı����Ϊ��2(8��6��6��2��8��2)��2(4��2��2��4��4��4)��2��4��2��200(mm2)��
���������ͼ�εı����Ϊ200mm2.
�����͡������
��������
7
��ͼ��ij��վ���ͻ����ƽ��ʾ��ͼ. Ϊ����ߴ����̵İ�ȫ�ԣ�����ʦ������С���ʹ������ļнǣ�ʹ����45���Ϊ30��. ��֪ԭ���ʹ�AB��Ϊ4��.
��1�����´��ʹ�AC�ij��ȣ�
��2�������Ҫ�ڻ����ŵص�C���������2��ͨ�������жϾ���B��4�Ļ��� �Ƿ���ҪŲ�ߣ���˵�����ɣ�
�Ƿ���ҪŲ�ߣ���˵�����ɣ�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�����а�����2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��֪�������εı߳�Ϊ2������������Բ�İ뾶Ϊ( )
A. 1 B.  C. 2
C. 2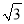 D. 2
D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧ��ģ�Ծ� ���ͣ������
��ͼ����֪��P�İ뾶Ϊ2��Բ��P��������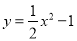 ���˶�������P��x������ʱ��Բ��P������Ϊ_____________
���˶�������P��x������ʱ��Բ��P������Ϊ_____________
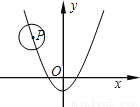
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ �������� ���ͣ������
��ͼ���ֱ��ǿɻ�����κ�ƽ���ı���ѧ�ߣ���֪ƽ���ı��ν϶̵ı������εı߳���ȣ�
��1����һ����ѧ��У�ijС��ѧ�������ε�һ����ƽ���ı��ν϶̱��غϣ���ƴ����ͼ1��ʾ��ͼ�Σ�AF������C������DE��AF�ڵ�M���۲췢�֣���M��DE���е㣮
��������λѧ���д����Ե�֤��˼·��
˼·1�������������ߣ�ֱ��֤������ȫ�ȣ�
˼·2����֤������ȫ�ȣ�����BD��AF�ڵ�H����
��ο������˼·��֤����M��DE���е㣨ֻ����һ�ַ���֤������
��2����ͼ2���ڣ�1����ǰ���£�����ABE=135��ʱ���ӳ�AD��EF���ڵ�N����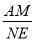 ��ֵ��
��ֵ��
��3���ڣ�2���������£���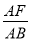 =k��kΪ����
=k��kΪ����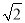 �ij�������ֱ���ú�k�Ĵ���ʽ��ʾ
�ij�������ֱ���ú�k�Ĵ���ʽ��ʾ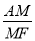 ��ֵ��
��ֵ��
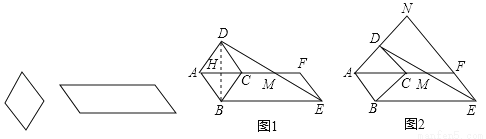
���𰸡���1��֤������������2��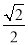 ����3��
����3��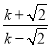 ��
��
�������������������1��֤��һ�������������ʵ�AB=CD��AB��CD������ƽ���ı��ε����ʵ�AB=EF��AB��EF����CD=EF��CD��EF���ٸ���ƽ���ߵ����ʵá�CDM=��FEM����ɸ��ݡ�AAS���жϡ�CDM�ա�FEM������DM=EM��
֤�����������������ʵ�DH=BH������ƽ���ı��ε����ʵ�AF��BE���ٸ���ƽ���߷��߶γɱ��������õ�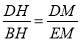 =1������DM=EM��
=1������DM=EM��
��2���ɡ�CDM�ա�FEM�õ�CM=FM����AD=a��CM=b����FM=b��EF=AB=a����֤���ı���ABCDΪ�����εõ�AC=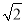 a������֤����ANFΪ����ֱ�������εõ�NF=a+
a������֤����ANFΪ����ֱ�������εõ�NF=a+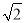 b����NE=NF+EF=2a+
b����NE=NF+EF=2a+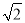 b��Ȼ�����
b��Ȼ�����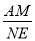 ��ֵ��
��ֵ��
��3������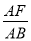 =
=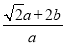 =
=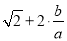 =k����
=k����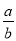 =
=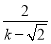 ��Ȼ���ʾ��
��Ȼ���ʾ��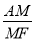 =
=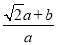 =
=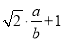 ���ٰ�
���ٰ�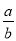 =
=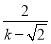 ������㼴�ɣ�
������㼴�ɣ�
�����������������
��1����ͼ1��֤��һ�����ı���ABCDΪ���Σ���AB=CD��AB��CD�����ı���ABEFΪƽ���ı��Σ���AB=EF��AB��EF����CD=EF��CD��EF�����CDM=��FEM���ڡ�CDM�͡�FEM�У��ߡ�CMD=��FME����CDM=��FEM��CD=EF�����CDM�ա�FEM����DM=EM������M��DE���е㣻
֤���������ı���ABCDΪ���Σ���DH=BH�����ı���ABEFΪƽ���ı��Σ���AF��BE����HM��BE���� 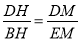 =1����DM=EM������M��DE���е㣻
=1����DM=EM������M��DE���е㣻
��2���ߡ�CDM�ա�FEM����CM=FM����AD=a��CM=b���ߡ�ABE=135�㣬���BAF=45�㣬���ı���ABCDΪ���Σ����NAF=45�㣬���ı���ABCDΪ�����Σ���AC=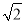 AD=
AD=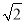 a����AB��EF�����AFN=��BAF=45�㣬���ANFΪ����ֱ�������Σ���NF=
a����AB��EF�����AFN=��BAF=45�㣬���ANFΪ����ֱ�������Σ���NF=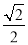 AF=
AF=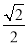 ��
��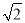 a+b+b��=a+
a+b+b��=a+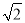 b����NE=NF+EF=a+
b����NE=NF+EF=a+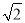 b+a=2a+
b+a=2a+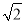 b����
b����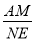 =
=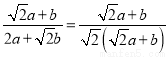 =
=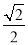 ��
��
��3����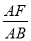 =
=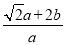 =
=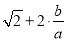 =k����
=k����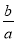 =
=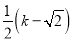 ����
����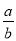 =
=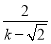 ����
����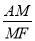 =
=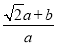 =
=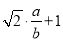 =
=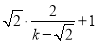 =
=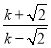 ��
��
�㾦�����⿼���������ε��ۺ��⣺��������ƽ���߷��߶γɱ���������ƽ���ı��κ����ε����ʣ��������ȫ�������ε�֪ʶ����߶���ȵ����⣻�����ô�������ʾ�߶�֮��Ĺ�ϵ��
�����͡������
��������
19
���ⱳ��
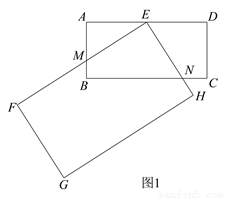
����ѧ����ϣ�����ʦҪ��ͬѧ�������Ŵ�С��ͬ�ľ���ֽƬ������ת�任̽�������ͼ 1���ھ���ֽƬABCD �;���ֽƬEFGH�У�AB��1��AD��2����FE��AD��FG��AB����E �� AD ���е㣬����ֽƬ EFGH �Ե�E Ϊ��ת���Ľ�����ʱ����ת������ת�����л����������������ϵ�����ǡ������ѧ���Ⲣ���Խ����
�������
����������ѧϰС���������ѧ���⣬��������Щ���⣮
��1�����ܽ���С������������ǣ���ͼ 1���� EF �� AB �ཻ�ڵ� M��EH �� BC �ཻ�ڵ� N ʱ����֤��EM=EN��
��2������ӥ��С������������ǣ��ڣ�1���������£��� AM=CN ʱ��AM �� BM ��������������ϵ����˵�����ɣ�
��3�������¡�С������������ǣ������� EFGH �����Ե� E Ϊ��ת���Ľ�����ʱ����ת���� 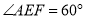 ʱ��������ͼ 2 �л�����ת���ʾ��ͼ���������ʱ EF ���� BC �ֳɵ������߶εij��ȣ�
ʱ��������ͼ 2 �л�����ת���ʾ��ͼ���������ʱ EF ���� BC �ֳɵ������߶εij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ �������� ���ͣ������
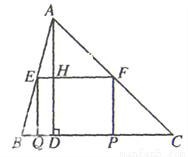
��ͼ���ڡ�ABC�У���C��45�㣬BC��10����AD��8������EFPQ��һ��QP��BC���ϣ�E��F����ֱ���AB��AC�ϣ�AD��EF�ڵ�H��
��1����֤�� 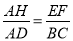 ��
��
��2����EF��x����xΪ��ֵʱ������EFPQ���������������ֵ��
��3��������EFPQ��������ʱ���þ���EFPQ��ÿ��1����λ���ٶ�������QC�����˶�������Q���C�غ�ʱֹͣ�˶��������˶�ʱ��Ϊt�룬����EFFQ���ABC�ص����ֵ����ΪS����S��t�ĺ�����ϵʽ��
���𰸡���1��֤������������2����x��5ʱ��S����EFPQ�����ֵ�����ֵΪ20����3��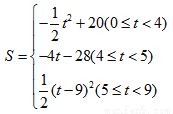
�������������������1�������������������ε����ʡ������������εĶ�Ӧ���ϵĸ�֮�ȵ������ƱȽ������2�����ݵ�һ�ʵĽ��ۣ����ɸ��ݾ��ε������ʽ�õ����ھ���EFPQ�������x�ĺ�����ϵʽ�����ݺ��������ʼ��ɵõ����ε�����������Ӧ��x��ֵ����3������Ҫ���弸���ؼ��㣬�����ε�������ʱ���ɣ�2����֪��ʱEF=5��EQ=4����֤�á�CPF�ǵ���Rt������PC=PF=4��QC=QP+PC=9��
һ��P��C�غ�ʱ�������ƶ��ľ���ΪPC����4�����˶���ʱ��Ϊ4s��
����E���߶�AC��ʱ�������ƶ��ľ���Ϊ9-4=5���˶���ʱ��Ϊ5s��
����Q��C�غ�ʱ�������˶��ľ���ΪQC����9�����˶���ʱ��Ϊ9s��
���Ա���Ҫ������������ֱ�д������ʽ����.
���������
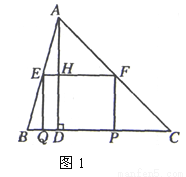
��1���� �ı���EFPQ�Ǿ��Σ��� EF��QP���� ��AEF�ס�ABC��
�֡� AD��BC��
�� AH��EF,��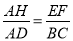
��2���ɣ�1����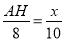 ���� AH��
���� AH��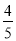 x��
x��
�� EQ��HD��AD��AH��8��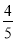 x��
x��
�� S����EFPQ��EF��EQ��x (8��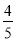 x) ����
x) ����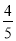 x2��8 x����
x2��8 x����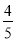 ��x��5��2��20��
��x��5��2��20��
�� ��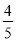 ��0�� �� ��x��5ʱ��S����EFPQ�����ֵ�����ֵΪ20��
��0�� �� ��x��5ʱ��S����EFPQ�����ֵ�����ֵΪ20��
��3����ͼ1���ɣ�2��
��EF��5��EQ��4��
�ߡ�C��45�㣬�� ��FPC�ǵ���ֱ�������Σ�
�� PC��FP��EQ=4��QC��QP��PC��9��
������������ۣ��� ��ͼ2����0��t��4ʱ��
��EF��PF�ֱ�AC�ڵ�M��N�����MFN�ǵ���ֱ��������,
�� FN��MF��t��
��S��S����EFPQ��SRt��MFN=20��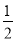 t2����
t2����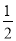 t2��20��
t2��20��
����ͼ3����4��t<5ʱ����ME��5��t��QC��9��t��
�� S��S����EMCQ��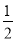 [��5��t������9��t ��]��4����4t��28��
[��5��t������9��t ��]��4����4t��28��
����ͼ4����5��t��9ʱ����EQ��AC�ڵ�K����KQ=QC��9��t��
�� S��S��KQC=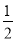 (9��t)2��
(9��t)2��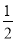 ( t��9)2��
( t��9)2��
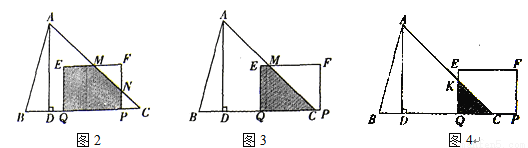
����������S��t�ĺ�����ϵʽΪ��
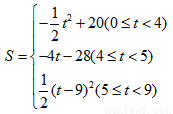
�㾦��������Ҫ�����˾��Ρ�����ֱ�������ε����ʣ����������ε��ж������ʼ����κ�����Ӧ�õ�֪ʶ��ͬʱ�������˷������۵���ѧ˼�룮
�����͡������
��������
12
��֪����x��һԪ���η���x2����2k��1��x��k2��2k��0������ʵ����x1��x2��
��1����ʵ��k��ȡֵ��Χ��
��2���Ƿ����ʵ��k��ʹ��x1��x2��x12��x22��0�����������ڣ������k��ֵ���������ڣ���˵�����ɣ�
(1)��k��ʱ��ԭ����������ʵ����(2)������ʵ��k��ʹ��x1��x2��x12��x22��0���� �������������������1������һԪ���η��̸����б�ʽ�г�����ʽ����֮���ɣ���2����������Τ�ﶨ�����. ��������� ��1�� ����� ��2���� �� �ɸ���ϵ���Ĺ�ϵ�ɵã� ����ã� �� ����ã� �� ��. ���ڵ�ȡֵ��ΧΪ�� �ʲ�����kʹ�� ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ �������� ���ͣ������
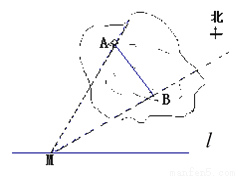
С����֪����������СͤA��B֮��ľ��룬������СͤA��Bλ��ͬһˮƽ���Ҷ�������ĺ���С��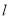 ��ijһ�۲��M�������ͤA�ڵ�M�ı�ƫ��30�㷽��, ͤB�ڵ�M�ı�ƫ��60�㷽��,��С���ɵ�M��С��
��ijһ�۲��M�������ͤA�ڵ�M�ı�ƫ��30�㷽��, ͤB�ڵ�M�ı�ƫ��60�㷽��,��С���ɵ�M��С��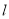 ����60��ʱ�������N������ʱ���ͤAǡ��λ�ڵ�N����������������30��ʱ�����Q������ʱͤBǡ��λ�ڵ�Q���������������ϲ������ݣ��������С�������������СͤA��B֮��ľ��룮
����60��ʱ�������N������ʱ���ͤAǡ��λ�ڵ�N����������������30��ʱ�����Q������ʱͤBǡ��λ�ڵ�Q���������������ϲ������ݣ��������С�������������СͤA��B֮��ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ������
ij�����ֻ�����Ϣ�����У��Ƚ���Ϣת��Ϊ������ 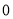 ��
�� 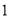 ��ɵ����ִ����������ִ����м��ܺ��ٴ��䣮�ֲ���һ�ּļ��ܷ�������ԭ�е�ÿ��
��ɵ����ִ����������ִ����м��ܺ��ٴ��䣮�ֲ���һ�ּļ��ܷ�������ԭ�е�ÿ�� 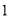 �����
����� 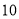 ��ԭ�е�ÿ��
��ԭ�е�ÿ��  �����
�����  ��������
��������  ��ʾû�о������ܵ����ִ���������
��ʾû�о������ܵ����ִ��������� 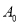 ����һ�μ��ܾ͵õ�һ���µ����ִ�
����һ�μ��ܾ͵õ�һ���µ����ִ�  ����
����  �ٽ���һ�μ����ֵõ�һ���µ����ִ�
�ٽ���һ�μ����ֵõ�һ���µ����ִ� 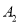 ���������ƣ�
���������ƣ�  ������
������  ��
��  ����
���� 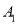 ��
��  ������֪
������֪ 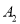 ��
��  ����
���� 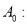 ________________�������ִ�
________________�������ִ� 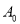 ����
���� 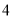 �����֣������ִ�
�����֣������ִ� 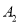 ����������������ȵ�����������________________�ԣ�
����������������ȵ�����������________________�ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ���ѡ��
Сǿ�����������С33�꣬�������������������Сǿ��4����Сǿ�����������
A. 10�� B. 11�� C. 12�� D. 13��
B ���������������� ��Сǿ������Ϊx�꣬�����������Ϊ4 x�꣬������ã�4 x - x =33����ã�x =11����ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶��ʦ�����ѧ�Ծ���B���� ���ͣ������
�ⷽ���飺  ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com