练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    点M（1，2）关于y轴对称点的坐标为（ ）

    A．（﹣1，2） B．（﹣1，﹣2） C．（1，﹣2） D．（2，﹣1）

    A 【解析】 试题分析：根据关于y轴对称的点，纵坐标相同，横坐标互为相反数解答． 【解析】 点M（1，2）关于y轴对称点的坐标为（﹣1，2）． 故选A．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型：解答题

    如图，M是线段AC中点，点B在线段AC上，且AB=4cm，BC=2AB，求线段MC和线段BM的长．

    BM= 2cm． 【解析】试题分析：由题意可得BC的长，从而得AC=AB+BC=12，根据M是线段AC的中点求得CM的长，利用BC-CM求得BM的长。 试题解析：∵AB=4，∴BC=2AB=8，∴AC=AB+BC=12，∵M是线段AC的中点，∴CM=AB=6，∴BM=BC-CM=2；即MC﹦6cm，BM﹦2cm .

    查看答案和解析>>

    科目：初中数学 来源：四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型：单选题

    在平面直角坐标系中，以点（3，2）为圆心，2为半径的圆与坐标轴的位置关系为（　　）

    A. 与x轴相离、与y轴相切 B. 与x轴、y轴都相离

    C. 与x轴相切、与y轴相离 D. 与x轴、y轴都相切

    C 【解析】试题解析：∵是以点(2,3)为圆心，2为半径的圆， 则有2=2，3>2， ∴这个圆与x轴相切，与y轴相离. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：填空题

    若x2+mx+4是完全平方式，则m=_____．

    ±4 【解析】这里首末两项是2x和2这两个数的平方，那么中间一项为加上或减去2x和2积的2倍，依此求出m的值． 【解析】 ∵x2+mx+4是一个完全平方式， ∴这两个数2x和2， ∴mx=±2×2?x， 解得m=±4． 故答案为：±4．

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：单选题

    下列从左到右的运算是因式分解的是( )

    A. 2a2﹣2a+1=2a（a﹣1）+1 B. （x﹣y）（x+y）=x2﹣y2

    C. 9x2﹣6x+1=（3x﹣1）2 D. x2+y2=（x﹣y）2+2xy

    C 【解析】A.没把一个多项式转化成几个整式积的形式，故A错误； B、是整式的乘法，故B错误； C、把一个多项式转化成几个整式积的形式，故C正确； D、没把一个多项式转化成几个整式积的形式，故D错误； 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：解答题

    某物流公司的快递车和货车同时从甲地出发，匀速向乙地行驶，快递车的速度为100km/h，货车的速度为60km/h，结果快递车比货车早2h到达乙地．快递车到达乙地后卸完物品再另装货物共用30min，立即按原路以90km/h速度匀速返回，直至与货车相遇．设两车之间的距离y（km）．货车行驶时间为x（h）．

    （1）求甲、乙两地之间的距离．

    （2）求快递车返回时y与x之间的函数关系式．

    （3）建立适当的坐标系画出y与x之间的函数图象．

    （1）300km；（2）y=﹣150x+615（3≤x≤4）．（3）见解析. 【解析】试题分析：（1）设甲、乙两地之间的距离为skm，根据时间=路程÷速度结合快递车比货车早2h到达乙地，即可得出关于s的一元一次方程，解之即可得出结论； （2）先求出快递车离开乙地的时间以及此时两车间的距离，再根据路程=初始距离-两车速度和×行驶时间，即可得出快递车返回时y与x之间的函数关系式，找出x的取...

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：填空题

    如图，在平面直角坐标系中，抛物线y=x2﹣x与x轴交于点A，点P在抛物线上，连结AP．若△OAP是以OA为底边的等腰三角形，则△OAP的面积是_____．

    【解析】令y=0,则x2?x=0，解得x=0或2， ∴点A坐标(2,0)， ∵△OAP是以OA为底边的等腰三角形， ∴点P是抛物线顶点， ∴点P坐标(1,? )， ∴S△OAP=×2×=.

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省平凉市中考数学模拟试卷 题型：解答题

    十八届五中全会出台了全面实施一对夫妇可生育两个孩子的政策，这是党中央站在中华民族长远发展的战略高度作出的促进人口长期均衡发展的重大举措．二孩政策出台后，某家庭积极响应政府号召，准备生育两个小孩（生男生女机会均等，且与顺序有关）．

    （1）该家庭生育两胎，假设每胎都生育一个小孩，求这两个小孩恰好是1男1女的概率；

    （2）该家庭生育两胎，假设第一胎生育一个小孩，且第二胎生育一对双胞胎，求这三个小孩中至少有1个女孩的概率．

    （1） （2） 【解析】（1）画树状图列出所有等可能结果，根据概率公式计算可得； （2）第一胎有男、女两种可能，第二胎由男男、男女、女男、女女四种可能，据此画出树状图，根据概率公式计算可得． 【解析】 （1）画树状图如下： 由树状图可知，生育两胎共有4种等可能结果，而这两个小孩恰好是1男1女的有2中可能， ∴P（恰好是1男1女的）=． （2）画树状图如下： ...

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省定安县中考数学仿真试卷（二） 题型：单选题

    点A（x1，y1）、B（x2，y2）在函数y=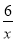的图象上，若0＜x2＜x1，则y1、y2的大小关系是（　　）

    A. y2＜y1 B. y1=y2

    C. y1＜y2 D. y1、y2的大小关系不确定

    C 【解析】∵y= ， ∴函数图象在第一、三象限，且在每个象限内，y随x的增大而减小， ∵点A（x1，y1）、B（x2，y2）在函数y= 的图象上，若0＜x2＜x1， ∴y1＜y2， 故选C．

    查看答案和解析>>

    同步练习册答案