练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    十八届五中全会出台了全面实施一对夫妇可生育两个孩子的政策，这是党中央站在中华民族长远发展的战略高度作出的促进人口长期均衡发展的重大举措．二孩政策出台后，某家庭积极响应政府号召，准备生育两个小孩（生男生女机会均等，且与顺序有关）．

    （1）该家庭生育两胎，假设每胎都生育一个小孩，求这两个小孩恰好是1男1女的概率；

    （2）该家庭生育两胎，假设第一胎生育一个小孩，且第二胎生育一对双胞胎，求这三个小孩中至少有1个女孩的概率．

    （1） （2） 【解析】（1）画树状图列出所有等可能结果，根据概率公式计算可得； （2）第一胎有男、女两种可能，第二胎由男男、男女、女男、女女四种可能，据此画出树状图，根据概率公式计算可得． 【解析】 （1）画树状图如下： 由树状图可知，生育两胎共有4种等可能结果，而这两个小孩恰好是1男1女的有2中可能， ∴P（恰好是1男1女的）=． （2）画树状图如下： ...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型：解答题

    如图，正方形网格中，△ABC为格点三角形（顶点都是格点），将△ABC绕点A按逆时针方向旋转90°得到△AB1C1．

    （1）在正方形网格中，作出△AB1C1；（不要求写作法）

    （2）设网格小正方形的边长为1cm，用阴影表示出旋转过程中线段BC所扫过的图形，然后求出它的面积．（结果保留π）．

    (1)作图见解析；（2）cm2 【解析】 试题分析：（1）根据网格图知：AB=4，BC=3，由勾股定理得，AC=5，作B1A⊥AB，且B1A=AB，作C1A⊥ABC且C1A=AC； （2）阴影部分的面积等于扇形ACC1与△ABC的面积和减去扇形ABB1与△AB1C1，而△ABC与△AB1C1的面积相等，∴阴影部分的面积等于扇形ACC1减去扇形ABB1的面积． 试题解析：（1...

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：单选题

    点M（1，2）关于y轴对称点的坐标为（ ）

    A．（﹣1，2） B．（﹣1，﹣2） C．（1，﹣2） D．（2，﹣1）

    A 【解析】 试题分析：根据关于y轴对称的点，纵坐标相同，横坐标互为相反数解答． 【解析】 点M（1，2）关于y轴对称点的坐标为（﹣1，2）． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：填空题

    计算： =_____．

    - 【解析】原式= .

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：单选题

    2016年10月17日，神州十一号飞船成功发射升空.发射当天约有161000个相关精彩栏目的热门视频在网络上热播.将数据161000用科学记数法表示为

    A. 1.61×103 B. 0.161×105 C. 1.61×105 D. 16.1×104

    C 【解析】科学记数法的表示形式为a×10n的形式．其中1≤|a|＜10，n为整数，确定n的值时，用原数的整数位数减1，即161000=1.61×105．故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省平凉市中考数学模拟试卷 题型：解答题

    如图，在平面直角坐标系中，过点A（2，0）的直线l与y轴交于点B，tan∠OAB=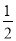，直线l上的点P位于y轴左侧，且到y轴的距离为1．

    （1）求直线l的表达式；

    （2）若反比例函数的图象经过点P，求m的值．

    （1）；（2）． 【解析】试题分析：(1)已知A（2，0）an∠OAB==,可求得OB=1，所以B（0，1），设直线l的表达式为，用待定系数法即可求得直线l的表达式；（2）根据直线l上的点P位于y轴左侧，且到y轴的距离为1可得点P的横坐标为－１，代入一次函数的解析式求得点P的纵坐标，把点P的坐标代入反比例函数中，即可求得m的值. 试题解析：(1) ∵A（2，0），∴OA=2. ∵...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省平凉市中考数学模拟试卷 题型：填空题

    如图，如图，点A（3，m）在第一象限，OA与x轴所夹的锐角为∠1，tan∠1=，则m的值是_____．

    2 【解析】作AB⊥x轴于点B． ∵A的坐标是（3，m）， ∴OB=3，AB=m． 又∵tan∠1=，即， ∴m=2．

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省定安县中考数学仿真试卷（二） 题型：解答题

    如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=80m，DE=10m，求障碍物B，C两点间的距离（结果精确到0.1m）（参考数据： ≈1.414， ≈1.732）

    障碍物B，C两点间的距离约为52.7m． 【解析】试题分析：如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H．通过解直角△AFD得到DF的长度；通过解直角△DCE得到CE的长度，则BC=BE-CE． 试题解析：如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H． 则DE=BF=CH=10m， 在直角△ADF中，∵AF=80m-10m=70m，∠ADF=45°，...

    查看答案和解析>>

    科目：初中数学 来源：重庆市校2018届九年级上学期期末模拟数学试卷 题型：单选题

    若二次函数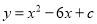的图象过三点，则大小关系正确的是（）

    A. B. C. D.

    B 【解析】试题解析：∵二次函数y=x2-6x+c， ∴该二次函数的抛物线开口向上，且对称轴为：x=3． ∵点（-1，y1）、（2，y2）、（5，y3）都在二次函数y=x2-6x+c的图象上， 而三点横坐标离对称轴x=3的距离按由远到近为： （-1，y1）、（5，y3）、（2，y2）， ∴y2＜y3＜y1 故选B．

    查看答案和解析>>

    同步练习册答案