练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若x2+mx+4是完全平方式，则m=_____．

    ±4 【解析】这里首末两项是2x和2这两个数的平方，那么中间一项为加上或减去2x和2积的2倍，依此求出m的值． 【解析】 ∵x2+mx+4是一个完全平方式， ∴这两个数2x和2， ∴mx=±2×2?x， 解得m=±4． 故答案为：±4．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年湖北省武汉市中考数学模拟试卷二 题型：单选题

    下列说法正确的是（　　）

    A. 符号相反的两个数是相反数

    B. 任何一个负数都小于它的相反数

    C. 任何一个负数都大于它的相反数

    D. 0没有相反数

    B 【解析】A. 符号相反的两个数是相反数，错误，如-1与5的符号相反，但不是相反数； B. 任何一个负数都小于它的相反数，正确，因为负数的相反数是正数，而负数小于正数； C. 任何一个负数都大于它的相反数，错误，任何一个负数都小于它的相反数； D. 0没有相反数，错误，0的相反数是0. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型：解答题

    如图，正方形网格中，△ABC为格点三角形（顶点都是格点），将△ABC绕点A按逆时针方向旋转90°得到△AB1C1．

    （1）在正方形网格中，作出△AB1C1；（不要求写作法）

    （2）设网格小正方形的边长为1cm，用阴影表示出旋转过程中线段BC所扫过的图形，然后求出它的面积．（结果保留π）．

    (1)作图见解析；（2）cm2 【解析】 试题分析：（1）根据网格图知：AB=4，BC=3，由勾股定理得，AC=5，作B1A⊥AB，且B1A=AB，作C1A⊥ABC且C1A=AC； （2）阴影部分的面积等于扇形ACC1与△ABC的面积和减去扇形ABB1与△AB1C1，而△ABC与△AB1C1的面积相等，∴阴影部分的面积等于扇形ACC1减去扇形ABB1的面积． 试题解析：（1...

    查看答案和解析>>

    科目：初中数学 来源：四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型：单选题

    方程x2+6x-5=0的左边配成完全平方后，得到的方程为（    ）.

    A. (x+3)2=14 B. (x-3)2=14 C. (x+6)2=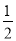 D. 以上都不对

    A 【解析】试题解析： 故选A.

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：解答题

    （1）画出△ABC关于y轴对称的图形△A1B1C1；

    （2）在x轴上找出点P，使得点P到点A、点B的距离之和最短（保留作图痕迹）

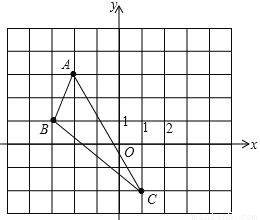
    见解析 【解析】 试题分析：（1）分别作出点A、B、C关于y轴对称的点，然后顺次连接； （2）作点B关于x轴的对称点B'，然后连接AB'，与x轴的交点即为点P． 【解析】 （1）（2）所作图形如图所示： ．

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：单选题

    已知：如图，∠1＝∠2，则不一定能使△ABD≌△ACD的条件是 （ ）

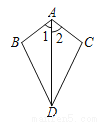
    A. AB＝AC B. BD＝CD C. ∠B＝∠C D. ∠BDA＝∠CDA

    B 【解析】试题分析：利用全等三角形判定定理ASA，SAS，AAS对各个选项逐一分析即可得出答案． 【解析】 A、∵∠1=∠2，AD为公共边，若AB=AC，则△ABD≌△ACD（SAS）；故A不符合题意； B、∵∠1=∠2，AD为公共边，若BD=CD，不符合全等三角形判定定理，不能判定△ABD≌△ACD；故B符合题意； C、∵∠1=∠2，AD为公共边，若∠B=∠C，则△A...

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：单选题

    点M（1，2）关于y轴对称点的坐标为（ ）

    A．（﹣1，2） B．（﹣1，﹣2） C．（1，﹣2） D．（2，﹣1）

    A 【解析】 试题分析：根据关于y轴对称的点，纵坐标相同，横坐标互为相反数解答． 【解析】 点M（1，2）关于y轴对称点的坐标为（﹣1，2）． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：填空题

    计算： =_____．

    - 【解析】原式= .

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省定安县中考数学仿真试卷（二） 题型：解答题

    如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=80m，DE=10m，求障碍物B，C两点间的距离（结果精确到0.1m）（参考数据： ≈1.414， ≈1.732）

    障碍物B，C两点间的距离约为52.7m． 【解析】试题分析：如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H．通过解直角△AFD得到DF的长度；通过解直角△DCE得到CE的长度，则BC=BE-CE． 试题解析：如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H． 则DE=BF=CH=10m， 在直角△ADF中，∵AF=80m-10m=70m，∠ADF=45°，...

    查看答案和解析>>

    同步练习册答案