
ij֯������ 180�����ˣ�Ϊ����߾���Ч�棬����������Ŀ����֪ÿ��ÿ����֯��30m����������֯������ 4 ��������һ����Ҫ�� 1.5m������ֱ�ӳ��ۣ�ÿ�ײ��ɻ��� 2 Ԫ�������Ƴ��º���ۣ�ÿ���ɻ��� 25 Ԫ����ÿ������ֻ����һ������Ҳ����������أ��谲�� x ���������£�
��1��һ���������������� Ԫ���ú� x ��ʽ��ʾ����
��2��һ��������ʣ��IJ���������Ϊ Ԫ���ú� x ��ʽ��ʾ����
��3��һ�쵱�а��� ����������ʱ����������Ϊ 13712 Ԫ��
��4��һ�갴 300 ����㣬һ����������������������ֵΪ����Ԫ��
��1��100x����2����10800-72x������3��104����4��4500000 Ԫ�� ����������1�� 25��4x=100x�� ��2�� 2[(180-x)��30-4��1.5x]=10800-72x�� ��3��10800-72x+100x=13712����ã�x=104�� ��4�� ��������ΪW��W=100x+10800-72x=28x+10800�� ��10800-72x��0...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��֪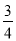 m��1=
m��1=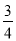 n�����õ�ʽ�����ʱȽ�m��n�Ĵ�С��
n�����õ�ʽ�����ʱȽ�m��n�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ��ȵ�һѧ�����п����꼶��ѧ�Ծ����𰸰棩 ���ͣ���ѡ��
���������в��ܱ�ʾ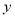 ��
��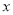 �ĺ������ǣ� ��
�ĺ������ǣ� ��
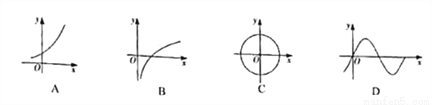
A. A B. B C. C D. D
C ��������A. ����x�ڵ�ÿһ��ȷ����ֵ��y����Ψһȷ����ֵ������Ӧ��y��x�ĺ�������A���������⣻ B. ����x�ڵ�ÿһ��ȷ����ֵ��y����Ψһȷ����ֵ������Ӧ��y��x�ĺ�������B���������⣻ C. ����x�ڵ�ÿһ��ȷ����ֵ��y��ʱ��2��ȷ����ֵ������Ӧ��y����x�ĺ�������C�������⣻ D. ����x�ڵ�ÿһ��ȷ����ֵ��y����Ψһȷ����ֵ������Ӧ��y��x�ĺ�������D��������...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ž���������2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ��������棩 ���ͣ������
��5���෴����_____��
5 ����������������� ���෴���� �ʴ�Ϊ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ž���������2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ��������棩 ���ͣ���ѡ��
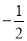 �ľ���ֵ���ڣ�������
�ľ���ֵ���ڣ�������
A. 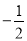 B. ��2 C.
B. ��2 C. 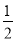 D. 2
D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�����꼶��ѧ �������� ���ͣ������
�Ķ��������,�ش�����.
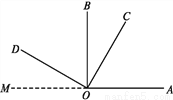
��ͼ,OC�ڡ�AOB��,��AOB�͡�COD����ֱ��,�ҡ�BOC=30��,���AOD�Ķ���.
��:��O��������OM,ʹ��M,O,A��ͬһֱ����.
��Ϊ��MOD+��BOD=90��,��BOC+��BOD=90��,���ԡ�BOC=��MOD,
���ԡ�AOD=180��-��BOC=180��-30��=150��.
(1)�����BOC=60��,��ô��AOD���ڶ��ٶ�?�����BOC=n��,��ô��AOD���ڶ��ٶ�?
(2)�����AOB=��DOC=x��,��AOD=y��,���BOC�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�����꼶��ѧ �������� ���ͣ������
��֪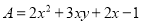 ��
�� 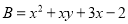 ��
��
��1����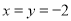 ʱ����
ʱ����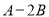 ��ֵ��
��ֵ��
��2����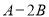 ��ֵ��
��ֵ��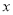 �أ���
�أ���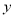 ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶�˽̰���ѧ�Ծ���B���� ���ͣ������
����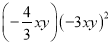 �Ľ��Ϊ__________��
�Ľ��Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�����СϪ����ѧ2017�������꼶��ѧ����ѧ�¼���� ���ͣ������
�Ȼ�������ֵ��4xy����2x2+5xy��y2��+2��x2+3xy��������x=��2��y=1��
��9 �������� �������������ȥ���ţ�Ȼ��ϲ�ͬ������ɰ���ʽ���л���Ȼ�������ֵ���㼴�ɣ� �������� ԭʽ=4xy��2x2��5xy+y2+2x2+6xy�� =5xy+y2�� ��x=��2��y=1ʱ��ԭʽ=5������2��+1=��9���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com