练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

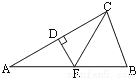
    如图，△ABC中，DE垂直平分AC交AB于E，∠A＝30°，∠ACB＝80°，则∠BCE的度数为（ ）

    A. 80° B. 70° C. 60° D. 50°

    D 【解析】因为DE垂直平分AC，所以EA=EC，∠A=∠ACE. 因为∠A＝30°，所以∠ACE=30°. 所以∠BCE=∠ACB-∠ACE=80°-30°=50°. 故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版九年级上册数学 22.1.2二次函数yax2的图象和性质 练习 题型：填空题

    已知二次函数y甲=mx2和y乙=nx2，对任意给定一个x值都有y甲≥y乙，关于m，n的关系正确的是_____(填序号).

    ①m<n<0 ②m>0，n<0 ③m<0，n>0 ④m>n>0

    ②④ 【解析】∵x2一定不小于0，则由条件“对应任意给定的x的值，都有y甲 y乙”可知：存在以下3种情况： （1）若y甲和y乙都为正数，则m＞0，n＞0且m＞n，即m>n>0； （2）若y甲为正数，y乙为负数，则m＞0，n＜0； （3）若都为负数时，则n＜m＜0； ∴关于m，n的关系正确的是② 、④ ．

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型：填空题

    如图,∠1=∠2,由AAS判定△ABD≌△ACD,则需添加的条件是_______.

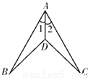
    ∠B=∠C 【解析】本题要判定△ABD≌△ACD，已知∠1=∠2，AD是公共边，具备了一边一角对应相等，注意“AAS”的条件；两角和其中一角的对应边相等，只能选∠B=∠C. 【解析】 由图可知，只能是∠B=∠C，才能组成“AAS”. 故填∠B=∠C.

    查看答案和解析>>

    科目：初中数学 来源：新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型：

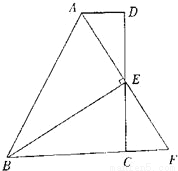
    如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．

    求证：（1）FC＝AD；

    （2）AB＝BC＋AD．

    （1）证明见解析；（2）证明见解析. 【解析】试题分析:（1）根据AD∥BC可知∠ADC=∠ECF，再根据E是CD的中点可求出△ADE≌△FCE，根据全等三角形的性质即可解答． （2）根据线段垂直平分线的性质判断出AB=BF即可． 证明：（1）∵AD∥BC（已知）， ∴∠ADC=∠ECF（两直线平行，内错角相等）， ∵E是CD的中点（已知）， ∴DE=EC（中点...

    查看答案和解析>>

    科目：初中数学 来源：新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型：

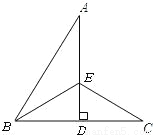
    如图，∠ABC＝50°，AD垂直且平分BC于点D，∠ABC的平分线BE交AD于点E，连接EC，则∠AEC的度数是（ ）

    A. 50° B. 25° C. 80° D. 115°

    D 【解析】因为AD垂直且平分BC，所以EB=EC，所以∠EBC=∠C. 因为BE平分∠ABC，所以∠ABC=2∠EBC=50°，所以∠EBC=25°，所以∠C=25°. 所以∠AEC=∠C+∠EDC=25°+90°=115°. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型：

    如图，直线CP是AB的中垂线且交AB于P，其中AP＝2CP．甲、乙两人想在AB上取两点D、E，使得AD＝DC＝CE＝EB，其作法如下：

    甲：作∠ACP、∠BCP之角平分线，分别交AB于D、E，则D、E即为所求；

    乙：作AC、BC之中垂线，分别交AB于D、E，则D、E即为所求．

    对于甲、乙两人的作法，下列判断何者正确（　　）

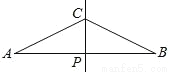
    A. 两人都正确 B. 两人都错误 C. 甲正确，乙错误 D. 甲错误，乙正确

    D 【解析】试题解析： 甲、乙都正确， 理由是：∵CP是线段AB的垂直平分线， ∴BC=AC，∠APC=∠BPC=90°， ∵AC=2CP， ∴∠A=30°， ∴∠ACP=60°， ∵CD平分∠ACP， ∴∠ACD=∠ACP=30°， ∴∠ACD=∠A， ∴AD=DC， 同理CE=BE， 即D、E为所求； ∵D在A...

    查看答案和解析>>

    科目：初中数学 来源：安徽省濉溪县2017-2018学年七年级上学期期中考试数学试卷 题型：解答题

    阅读下面的解题过程：

    解方程：|x+3|=2．

    【解析】
    当x+3≥0时，原方程可化成为x+3=2

    解得x=-1，经检验x=-1是方程的解；

    当x+3＜0，原方程可化为，-（x+3）=2

    解得x=-5，经检验x=-5是方程的解．

    所以原方程的解是x=-1，x=-5．

    解答下面的两个问题：

    （1）解方程：|3x-2|-4=0；

    探究：当值a为何值时，方程|x-2|=a， ①无解；②只有一个解；③有两个解．

    （1）x=2或x=-； (2) a小于0，无解；a=0，一个解；a大于0，两个解. 【解析】试题分析：（1）根据绝对值的性质，可化简绝对值，根据解方程，可得答案； （2）根据绝对值的性质，可得答案． 【解析】 （1）当3x﹣2≥0时，原方程可化为3x﹣2=4， 解得x=2，经检验x=2是方程的解； 当3x﹣2＜0时，原方程可化为﹣（3x﹣2）=4， 解得x=﹣...

    查看答案和解析>>

    科目：初中数学 来源：安徽省濉溪县2017-2018学年七年级上学期期中考试数学试卷 题型：单选题

    本学期我县义务教育阶段在校学生人数约为13.5万，数13.5万用科学计数法表示为（ ）

    (A) 13.5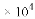 (B) 1.35 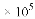(C) 0.135 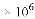(D) 135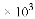

    B 【解析】试题解析：科学记数法表示数的标准格式为( ，且是整数)，所以135000用科学记数法表示应为，故本题应选B.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 24.2.2直线和圆的位置关系（2）练习 题型：解答题

    如图AB,AC是⊙O的两条弦，∠A＝30°，过点C的切线与OB的延长线交于点D，求∠D的度数．

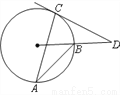
    30° 【解析】试题分析:连接OC,则∠OCD=90°,由圆周角定理可知, ∠COB=2∠A=60°, 即可求∠D=90°－∠COB=30°. 试题解析:连接OC, ∵CD是切线, ∴∠OCD＝90°, ∵∠A＝30°, ∴∠COD＝60°, ∴∠D＝30°.

    查看答案和解析>>

    同步练习册答案