练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在Rt△ABC中，∠C=90°，①若a=5，b=13，则c=________；②若a=9，c=41，则b=________．

    40． 【解析】【解析】 ①∠C=90°， 由勾股定理得：c= = = ； ②∠C=90°，由勾股定理得：b== =40； 故答案为： ；40．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省东台市2017-2018学年上学期期末考试九年级数学试卷 题型：填空题

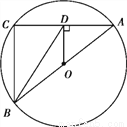
    如图，AB，AC分别是☉O的直径和弦，OD⊥AC于点D，连接BD，BC，AB=5，AC=4，则BD=____. 

    【解析】∵AB是⊙O的直径， ∴∠ACB=90°， 又∵AB=5，AC=4，OD⊥AC于点D， ∴BC=，CD=AC=2， ∴BD=. 即答案为.

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：解答题

    在创建全国森林城市的活动中，我区一“青年突击队”决定义务整修一条1000米长的绿化带，开工后，附近居民主动参加到义务劳动中，使整修的速度比原计划提高了一倍，结果提前4小时完成任务，问“青年突击队”原计划每小时整修多少米长的绿化带？

    原计划每小时整修125米长的绿化带． 【解析】试题分析：设原计划每小时整修x米长的绿化带，根据“计划时间-实际时间=4”这一等量关系列出方程，解方程即可得. 试题解析：设原计划每小时整修x米长的绿化带， 根据题意得： ， 解得：x=125， 经检验：x=125是原方程的解， ∴x=125 答：原计划每小时整修125米长的绿化带．

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：单选题

    满足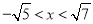的整数x有（     ）个

    A. 6个 B. 5个 C. 4个 D. 3个

    B 【解析】【解析】 由题意得： ＜≤x≤＜，∴满足条件的整数有-2，-1，0，1，2，共5个．故选B．

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：解答题

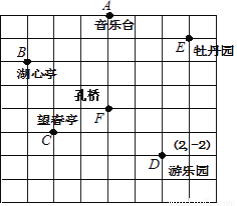
    王霞和爸爸、妈妈到人民公园游玩，回到家后，她利用平面直角坐标系画出了公园的景区地图，如图所示．可是她忘记了在图中标出原点和x轴．y轴．只知道游乐园D的坐标为（2，﹣2），请你帮她画出坐标系，并写出其他各景点的坐标．

    A（0，4），B（﹣3，2），C（﹣2，﹣1），E（3，3），F（0，0）． 【解析】试题分析：根据游乐园D的坐标为（2，-2）即可确定平面直角坐标系的位置，根据建立的平面直角坐标系即可写出各个点的坐标． 试题解析： 以F为坐标系原点，A（0，4） B（-3，2） C（-2，-1） E（3，3） F（0，0）

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：填空题

    分式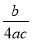与的最简公分母是________．

    12a2bc． 【解析】【解析】 找出各个因式的最高次幂，乘积就是分母的最简公分母．分式与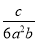的最简公分母是12a2bc．故答案为：12a2bc．

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：单选题

    已知方程组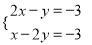 的解为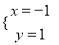，则函数y=2x+3与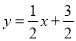的交点坐标为（     ）?

    A. （1，5） B. （-1，1）                               C. （1，2） D. （4，1）

    B 【解析】∵方程组的解为，∴函数y=2x+3与的交点坐标为（-1，1），故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型：解答题

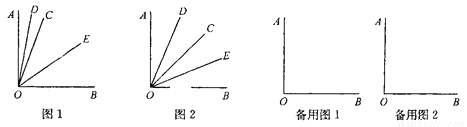
    已知∠AOB是一个直角，作射线OC，再分别作∠AOC和∠BOC的平分线OD，OE．

    (1) 如图1，当∠BOC=70°时，求∠DOE的度数．

    (2) 如图2，当射线OC在∠AOB内绕点O旋转时，∠DOE的大小是否发生变化?说明理由．

    (3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时，画出图形，直接写出相应的∠DOE的度数．(不必写出过程)

    (1)45°;(2)45°;(3) ∠DOE的大小发生变化.45°或135°. 【解析】试题分析： （1）因为∠DOE=∠COD+∠COE，所以分别根据角平分线的定义求出∠COD和∠COE即可； （2）因为∠DOE=∠COD+∠COE，结合角平分线即可求解； （3）需要分类，当∠AOC是钝角时和当∠AOC大于钝角时，结合角平分线求解. 试题解析： (1) 根据题...

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：单选题

    如图所示，△ABC中，AB=BC=AC，BD=CE，AD与BE相交于点P，则∠APE的度数是（   ）

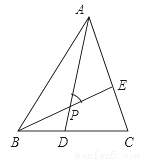
    A. 45° B. 55° C. 75° D. 60°

    D 【解析】在△ABD和△BCE中， ∴△ABD≌△BCE（SAS）， ∴∠BAD=∠CBE， ∵∠APE=∠ABE+∠BAD，∠ABE+∠CBE=60°， ∴∠APE=∠ABC=60°． 故选D．

    查看答案和解析>>

    同步练习册答案