
如图所示,△ABC中,AB=BC=AC,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
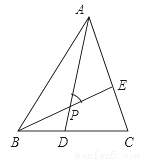
A. 45° B. 55° C. 75° D. 60°
D 【解析】在△ABD和△BCE中, ∴△ABD≌△BCE(SAS), ∴∠BAD=∠CBE, ∵∠APE=∠ABE+∠BAD,∠ABE+∠CBE=60°, ∴∠APE=∠ABC=60°. 故选D.科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:填空题
在Rt△ABC中,∠C=90°,①若a=5,b=13,则c=________;②若a=9,c=41,则b=________.
40. 【解析】【解析】 ①∠C=90°, 由勾股定理得:c= = = ; ②∠C=90°,由勾股定理得:b== =40; 故答案为: ;40.查看答案和解析>>
科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:填空题
11点整,时钟的分针与夹角是______。
30° 【解析】11点整时时针指向11,分针指向12,所以它们的夹角是30°. 故答案为30°.查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:解答题
如图所示的一块地,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m,求这块地的面积.
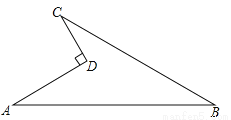
查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:单选题
下列计算正确的是( )
A. 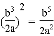 B.
B. 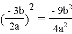
C. 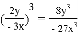 D.
D. 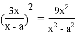
查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:填空题
使不等式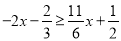 成立的最大的整数解是________.
成立的最大的整数解是________.
查看答案和解析>>
科目:初中数学 来源:2017年山东省中考数学二模试卷 题型:解答题
问题背景
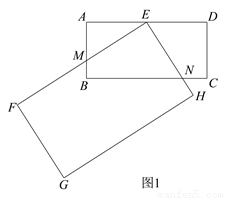
在数学活动课上,张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动.如图 1,在矩形纸片ABCD 和矩形纸片EFGH中,AB=1,AD=2,且FE>AD,FG>AB,点E 是 AD 的中点,矩形纸片 EFGH 以点E 为旋转中心进行逆时针旋转,在旋转过程中会产生怎样的数量关系,提出恰当的数学问题并加以解决.
解决问题
下面是三个学习小组提出的数学问题,请你解决这些问题.
(1)“奋进”小组提出的问题是:如图 1,当 EF 与 AB 相交于点 M,EH 与 BC 相交于点 N 时,求证:EM=EN.
(2)“雄鹰”小组提出的问题是:在(1)的条件下,当 AM=CN 时,AM 与 BM 有怎样的数量关系,请说明理由.
(3)“创新”小组提出的问题是:若矩形 EFGH 继续以点 E 为旋转中心进行逆时针旋转,当 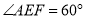 时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.
时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.

查看答案和解析>>
科目:初中数学 来源:2017年山东省中考数学二模试卷 题型:单选题
某红外线遥控器发出的红外线波长为0.000 00094m,用科学计数法表示这个数是( )
A. 9.4×10-7m B. 9.4×107m C. 9.4×10-8m D. 9.4×108m
A 【解析】试题分析:科学计数法是指:a×,且1≤<10,小数点向右移动几位,则n的相反数就是几.查看答案和解析>>
科目:初中数学 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:填空题
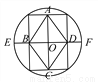
如图,顺次连接圆内接矩形各边的中点,得到菱形ABCD,若BD=10,DF=4,则菱形ABCD的边长为__ __.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com