
ЕЧОпПЯy=©Ѓ2ЈЁx+1Ј©2©Ѓ3µДїЄїЪПт_____Ј¬¶ФіЖЦбКЗ_____Ј¬¶ҐµгЧш±кКЗ_____Ј¬µ±x_____К±Ј¬yЛжxµДФцґу¶шјхРЎЈ¬µ±x_____К±Ј¬yУРЧо_____ЦµЈ¬КЗy=_____Ј®
ПВ x=©Ѓ1 ЈЁ©Ѓ1Ј¬©Ѓ3Ј© xЈѕ©Ѓ1 x=©Ѓ1 ґу -3 ЎѕЅвОцЎїКФМвЅвОцЈєЕЧОпПЯy=©Ѓ2ЈЁx+1Ј©2©Ѓ3µДїЄїЪПтПВЈ¬¶ФіЖЦбКЗЦ±ПЯx=©Ѓ1Ј¬¶ҐµгЧш±кКЗЈЁ©Ѓ1Ј¬©Ѓ3Ј©Ј¬µ±xЈѕ©Ѓ1К±Ј¬yЛжxµДФцґу¶шјхРЎЈ¬µ±x=©Ѓ1К±Ј¬yУРЧоґуЦµЈ¬КЗy=©Ѓ3Ј¬ №Кґр°ёОЄЈєПВЈ¬x=©Ѓ1Ј¬ЈЁ©Ѓ1Ј¬©Ѓ3Ј©Ј¬xЈѕ©Ѓ1Ј¬x=©Ѓ1Ј¬ґуЈ¬©Ѓ3
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈєЅЛХКЎДПѕ©КРБЄєПМе2018ЅмѕЕДкј¶ЙПС§ЖЪЖЪД©їјКФКэС§КФѕн МвРНЈєМоїХМв
ИзНјЈ¬ТСЦЄѕШРОABCDµД¶ҐµгAЎўD·Ц±рВдФЪxЦбЎўyЦбЈ¬OD=2OA=6Ј¬ADЈєAB=3Јє1Ј®ФтµгBµДЧш±кКЗ_______Ј®
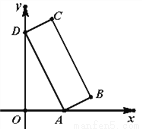
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє±±ѕ©ґуС§ёЅКфЦРС§2017-2018С§ДкЖЯДкј¶ЙПС§ЖЪЖЪЦРїјКФКэС§КФѕн МвРНЈєЅвґрМв
ТСЦЄ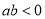 Ј¬
Ј¬ 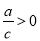 Ј¬ЗТ
Ј¬ЗТ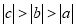 Ј¬КэЦбЙП
Ј¬КэЦбЙП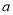 Ўў
Ўў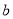 Ўў
Ўў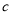 ¶ФУ¦µДµгКЗ
¶ФУ¦µДµгКЗ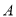 Ўў
Ўў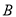 Ўў
Ўў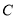 Ј®
Ј®
ЈЁ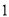 Ј©Иф
Ј©Иф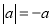 К±Ј¬ЗлФЪКэЦбЙП±кіц
К±Ј¬ЗлФЪКэЦбЙП±кіц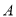 Ўў
Ўў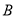 Ўў
Ўў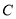 µДґуЦВО»ЦГЈє
µДґуЦВО»ЦГЈє
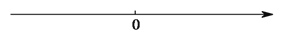
ЈЁ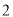 Ј©ФЪЈЁ
Ј©ФЪЈЁ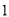 Ј©µДМхјюПВЈ¬»Їјт
Ј©µДМхјюПВЈ¬»Їјт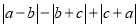 Ј®
Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє±±ѕ©ґуС§ёЅКфЦРС§2017-2018С§ДкЖЯДкј¶ЙПС§ЖЪЖЪЦРїјКФКэС§КФѕн МвРНЈєµҐСЎМв
ПВБРёчКЅјЖЛгХэИ·µДКЗЈЁ Ј©Ј®
A. 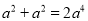 B.
B. 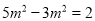 C.
C. 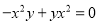 D.
D. 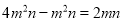
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈєМмЅтКР2018ЅмѕЕДкј¶ЈЁЙПЈ©µЪЛДЦЬЦЬЗеКэС§КФѕн МвРНЈєЅвґрМв
ТСЦЄ¶юґОєЇКэµДНјПуѕ№эµгЈЁЈ1Ј¬Ј5Ј©Ј¬ЈЁ0Ј¬Ј4Ј©єНЈЁ1Ј¬1Ј©.ЗуХвёц¶юґОєЇКэµДЅвОцКЅ.
ЎѕЅвОцЎїКФМв·ЦОцЈєТСЦЄБЛ¶юґОєЇКэНјПуѕ№эµДИэµгЧш±кЈ¬їЙУГґэ¶ЁПµКэ·ЁЗуіцЕЧОпПЯµДЅвОцКЅЈ® КФМвЅвОцЈє ЙиЛщЗуєЇКэµДЅвОцКЅОЄ °СЈЁЁD1Ј¬ЁD5Ј©Ј¬ЈЁ0Ј¬Ј4Ј©Ј¬ЈЁ1Ј¬1Ј©·Ц±рґъИлЈ¬ µГ Ј¬ ЅвХвёц·ЅіМЧйЈ¬ µГ ЛщЗуµДєЇКэµДЅвОцКЅОЄІйїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈєМмЅтКР2018ЅмѕЕДкј¶ЈЁЙПЈ©µЪЛДЦЬЦЬЗеКэС§КФѕн МвРНЈєµҐСЎМв
¶юґОєЇКэy=©Ѓ2ЈЁx©Ѓ1Ј©2+3µДНјПуµД¶ҐµгЧш±кКЗЈЁЎЎЎЎЈ©
A. ЈЁ1Ј¬3Ј© B. ЈЁ©Ѓ1Ј¬3Ј© C. ЈЁ1Ј¬©Ѓ3Ј© D. ЈЁ©Ѓ1Ј¬©Ѓ3Ј©
A ЎѕЅвОцЎїУЙ¶юґОєЇКэ¶ҐµгКЅЦЄЈ¬¶ҐµгКЗЈЁ1,3Ј©Ј¬СЎA.Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє№г¶«КЎ№гЦЭКРМмєУЗш2017-2018С§Дк°ЛДкј¶ЙПС§ЖЪЖЪД©їјКФКэС§КФѕн МвРНЈєЅвґрМв
ИзНјЈ¬µгDКЗЎчABC±ЯBCЙПТ»µгЈ¬AD=BDЈ¬ЗТADЖЅ·ЦЎПBAC.ЈЁ1Ј©ИфЎПB=50ЎгЈ¬ЗуЎПADCµД¶ИКэЈ»ЈЁ2Ј©ИфЎПC=30ЎгЈ¬ЗуЎПADCµД¶ИКэ.
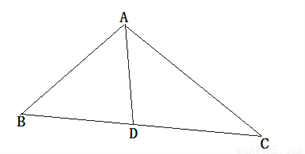
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє№г¶«КЎ№гЦЭКРМмєУЗш2017-2018С§Дк°ЛДкј¶ЙПС§ЖЪЖЪД©їјКФКэС§КФѕн МвРНЈєµҐСЎМв
ПВБРСЎПоЦРµДЖыіµЖ·ЕЖ±кЦѕНјЈ¬І»КЗЦб¶ФіЖНјРОµДКЗЈЁ Ј©
A.  B.
B.  C.
C.  D.
D. 
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈєєюДПКЎОдёФКР2017-2018С§Дк°ЛДкј¶ЙПС§ЖЪЖЪД©їјКФКэС§КФѕн МвРНЈєМоїХМв
ИфЅв·ЦКЅ·ЅіМ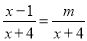 µДЅвОЄёєКэЈ¬Фт
µДЅвОЄёєКэЈ¬Фт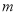 µДИЎЦµ·¶О§КЗ____
µДИЎЦµ·¶О§КЗ____
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com