练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    广佰文化商场同时卖出两台电子琴,每台均卖960元,以成本计算,其中一台盈利20%,另一台亏损20%,则本次出售中商场( )

    A. 不赔不赚 B. 赚160元 C. 赚80元 D. 赔80元

    D 【解析】试题分析：设两台电子琴的原价分别为x元与y元， 则第一台可列方程（1+20%）•x=960，解得：x=800． 比较可知，第一台赚了160元， 第二台可列方程（1-20%）•y=960，解得：y=1200元， 比较可知第二台亏了240元， 两台一合则赔了80元． 故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山西农业大学附属中学2017-2018学年八年级上学期第三次月考数学试卷 题型：单选题

    若(x－3)(x＋4)=x2＋px＋q，那么p、q的值是

    A. p=1，q=－12 B. p=－1，q=12

    C. p=7，q=12 D. p=7，q=－12

    A 【解析】试题分析：此题可以将等式左边展开和等式右边对照，根据对应项系数相等即可得到p、q的值． 由于（x-3）（x+4）=x2+x-12=x2+px+q，则p=1，q=-12． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：江西省抚州市2017-2018年上学期九年级数学期末试卷 题型：解答题

    由几个小立方体叠成的几何体的主视图和左视图如图所示，求组成几何体的小立方体个数的最大值与最小值，并画出相应的俯视图.

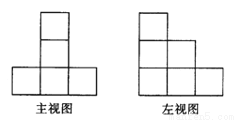
    最大值为12个，最小值为7个，俯视图分别如图所示. 【解析】试题分析：仔细观察该几何体的主视图和左视图，发挥空间想象能力，便可得出几何体的形状，最多时几何体的底层呈3×3=9个小正方体构成，然后根据主视图与左视图即可得到相应的俯视图（每个方格内的数字表示该位置上叠的小立方体的个数），也可以得出最少时如何摆放，从而可得. 试题解析：最大值为12个，最小值为7个，俯视图分别如图所示（每个方...

    查看答案和解析>>

    科目：初中数学 来源：广州市2018学年度七年级（上）数学期末测试卷 题型：解答题

    列方程解应用题

    (1)在“十一”期间，小明等同学随家长共15人到游乐园游玩，成人门票每张50元，学生门票是6折优惠．他们购票共花了650元，求一共去了几个家长、几个学生？

    (2)甲、乙两人骑自行车同时从相距65千米的两地出发相向而行，甲的速度是每小时17.5千米，乙的速度是每小时15千米，求经过几小时甲、乙两人相距32.5千米？

    （1）一共去了10个家长、5个学生．（2）经过1小时或3小时，甲、乙两人相距32．5千米． 【解析】试题分析：（1）设一共去了个家长，则去了个学生，根据总费用=成人购票的费用+学生购票的费用即可得出关于的一元一次方程，解之即可得出结论； （2）设经过小时，甲、乙两人相距32.5千米，根据路程=速度×时间即可得出关于的一元一次方程，解之即可得出结论． 试题解析：(1)设一共去了x个家长...

    查看答案和解析>>

    科目：初中数学 来源：广州市2018学年度七年级（上）数学期末测试卷 题型：填空题

    平面上任意两点确定一条直线，任意三点最多可确定3条直线，若平面上任意n个点最多可确定28条直线，则n的值是________________________

    8 【解析】试题解析：两点确定一条直线;不同三点最多可确定3条直线;不同4点最多可确定(1+2+3)条直线,不同5点最多可确定(1+2+3+4)条直线， 因为1+2+3+4+5+6+7=28， 所以平面上不同的8个点最多可确定28条直线. 故答案是：8.

    查看答案和解析>>

    科目：初中数学 来源：广州市2018学年度七年级（上）数学期末测试卷 题型：单选题

    已知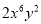和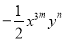是同类项，那么2m+n的值( )

    A. 3 B. 4 C. 5 D. 6

    D 【解析】试题解析：根据同类项的定义可知： 解得： 故选D.

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：解答题

    心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知， 学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB，BC分别为线段，CD为双曲线的一部分)．

    (1)开始上课后第5分钟时与第30分钟时相比较，何时学生的注意力更集中？

    (2)一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？

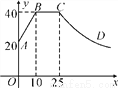
    (1)第30分钟注意力更集中；(2)老师能在学生注意力达到所需的状态下讲解完成这道题目. 【解析】试题分析：（1）先用代定系数法分别求出AB和CD的函数表达式，再分别求第五分钟和第三十分钟的注意力指数，最后比较判断. （2）分别求出注意力指数为36时的两个时间，再将两时间之差和19比较，大于19则能讲完，否则不能． 试题解析： (1)由题意得y1＝2x＋20(0≤x≤10)...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：单选题

    某机械厂七月份生产零件50万个，第三季度生产零件196万个．设该厂八、九月份平均每月

    的增长率为x，那么x满足的方程是 （ ）

    A. 50（1+x）2=196

    B. 50+50（1+x）2=196

    C. 50+50（1+x）+50（1+x）2=196

    D. 50+50（1+x）+50（1+2x）=196

    C 【解析】试题分析：设每月的平均增长率为x，七月份生产零件50万个，八月份生产零件50(1+x)万个，九月份生产零件50(1+x)2万个， 根据第三季度生产零件196万个可列方程为：50+50(1+x)+50(1+x)2=196． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市2017年中考二模试卷数学试卷 题型：解答题

    如图，反比例函数y=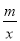的图象与一次函数y=kx+b的图象交于A、B两点，点A的坐标为（2，3n），点B的坐标为（5n+2，1）．

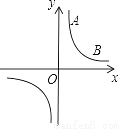
    （1）求反比例函数与一次函数的表达式；

    （2）将一次函数y=kx+b的图象沿y轴向下平移a个单位，使平移后的图象与反比例函数y= 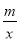的图象有且只有一个交点，求a的值；

    （3）点E为y轴上一个动点，若S△AEB=5，则点E的坐标为________．

    （0，6）或（0，8） 【解析】试题分析：（1）把点A的坐标、点B的坐标代入y＝，得出m、n的值，得出点A、B的坐标，再把A、B的坐标代入直线y＝kx＋b，求出k、b的值，从而得出一次函数的解析式； （2）设平移后的一次函数的解析式为y＝－x＋7－a，由一次函数解析式和反比例函数解析式联立组成二元方程组，消去y，得到关于x的一元二次方程，令△＝0即可求出a的值； （3）设点E的坐...

    查看答案和解析>>

    同步练习册答案