
如图是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为_米.(结果精确到0.1米,参考数据:  ≈1.41,
≈1.41,  ≈1.73)
≈1.73)

【答案】2.9
【解析】试题分析:在Rt△AMD中,∠MAD=45°,AM=4米,可得MD=4米;在Rt△BMC中,BM=AM+AB=12米,∠MBC=30°,可求得MC=4 米,所以警示牌的高CD=4
米,所以警示牌的高CD=4 -4=2.9米.
-4=2.9米.
考点:解直角三角形.
【题型】填空题
【结束】
16
如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=_____.

科目:初中数学 来源:广东省汕头市2018年中考数学模拟试卷(二) 题型:单选题
在同一坐标系中,一次函数y=ax+1与二次函数y=x2+a的图象可能是( )
A. 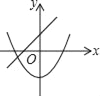 B.
B. 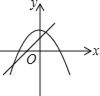 C.
C. 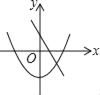 D.
D. 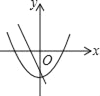
查看答案和解析>>
科目:初中数学 来源:北京市2018届初三数学中考复习 综合练习题 含答案 题型:解答题
解不等式组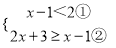 ,请结合题意填空,完成本题的解答.
,请结合题意填空,完成本题的解答.
(1)解不等式①,得________;
(2)解不等式②,得________;
(3)把不等式的解集在数轴上表示出来;
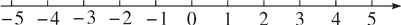
(4)不等式组的解集为__________.
查看答案和解析>>
科目:初中数学 来源:天津市2018届初三数学中考复习综合检测题 题型:解答题
已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.
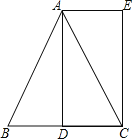
(1)求证:△ABD≌△CAE;
(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.
【答案】(1)证明详见解析;(2)AB∥DE,AB=DE,理由详见解析.
【解析】试题分析:(1)运用AAS证明△ABD≌△CAE;
(2)易证四边形ADCE是矩形,所以AC=DE=AB,也可证四边形ABDE是平行四边形得到AB=DE.
试题解析:证明:(1)∵AB=AC,
∴∠B=∠ACD,
∵AE∥BC,
∴∠EAC=∠ACD,
∴∠B=∠EAC,
∵AD是BC边上的中线,
∴AD⊥BC,
∵CE⊥AE,
∴∠ADC=∠CEA=90°
在△ABD和△CAE中
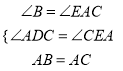
∴△ABD≌△CAE(AAS);
(2)AB∥DE,AB=DE,理由如下:
如图所示,
∵AD⊥BC,AE∥BC,
∴AD⊥AE,
又∵CE⊥AE,
∴四边形ADCE是矩形,
∴AC=DE,
∵AB=AC,
∴AB=DE,
∵AE∥BC,
∴四边形ABDE是平行四边形,
∴AB∥DE,AB=DE.
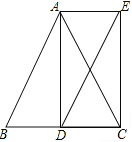
考点:全等三角形的判定与性质;等腰三角形的性质;平行四边形的判定与性质.
【题型】解答题
【结束】
21
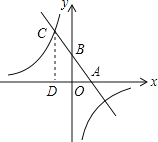
已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=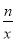 (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式;kx+b≤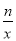 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源:天津市2018届初三数学中考复习综合检测题 题型:填空题
如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )

A.  B. AD,AE将∠BAC三等分
B. AD,AE将∠BAC三等分
C. △ABE≌△ACD D. S△ADH=S△CEG
【答案】A
【解析】试题解析:∵∠B=∠C=36°,∴AB=AC,∠BAC=108°,∵DH垂直平分AB,EG垂直平分AC,∴DB=DA,EA=EC,∴∠B=∠DAB=∠C=∠CAE=36°,∴△BDA∽△BAC,∴ ,又∵∠ADC=∠B+∠BAD=72°,∠DAC=∠BAC﹣∠BAD=72°,∴∠ADC=∠DAC,∴CD=CA=BA,∴BD=BC﹣CD=BC﹣AB,则
,又∵∠ADC=∠B+∠BAD=72°,∠DAC=∠BAC﹣∠BAD=72°,∴∠ADC=∠DAC,∴CD=CA=BA,∴BD=BC﹣CD=BC﹣AB,则 =
= ,即
,即 =
= ,故A错误;
,故A错误;
∵∠BAC=108°,∠B=∠DAB=∠C=∠CAE=36°,∴∠DAE=∠BAC﹣∠DAB﹣∠CAE=36°,即∠DAB=∠DAE=∠CAE=36°,∴AD,AE将∠BAC三等分,故B正确;
∵∠BAE=∠BAD+∠DAE=72°,∠CAD=∠CAE+∠DAE=72°,∴∠BAE=∠CAD,在△BAE和△CAD中,∵∠B=∠C,AB=AC,∠BAE=∠CAD,∴△BAE≌△CAD,故C正确;
由△BAE≌△CAD可得S△BAE=S△CAD,即S△BAD+S△ADE=S△CAE+S△ADE,∴S△BAD=S△CAE,又∵DH垂直平分AB,EG垂直平分AC,∴S△ADH= S△ABD,S△CEG=
S△ABD,S△CEG= S△CAE,∴S△ADH=S△CEG,故D正确.
S△CAE,∴S△ADH=S△CEG,故D正确.
故选A.
【题型】单选题
【结束】
11
红细胞是人体中血液运输氧气的主要媒介,人体中红细胞的直径约为0.0000077m,将0.0000077用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源:天津市2018届初三数学中考复习综合检测题 题型:单选题
下列运算正确的是( )
A. a2+4a-4=(a+2)2 B. a2+a2=a4
C. (-2ab)2=-4a2b2 D. a4÷a=a3
查看答案和解析>>
科目:初中数学 来源:四川省2018届九年级下学期二诊考试数学试卷 题型:填空题
如图,已知直线y= x+1与y轴交于点A,与x轴交于点D,抛物线y=
x+1与y轴交于点A,与x轴交于点D,抛物线y=  x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标__________.
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标__________.

查看答案和解析>>
科目:初中数学 来源:河南省周口市西华县2017-2018学年七年级下学期期中考试数学试卷 题型:解答题
如图,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H的位置,使它到四个村庄距离之和最小;
(2)计划把河水引入蓄水池H中,怎样开渠使渠道最短?说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com