
已知|2m-5|+(2m-5n+20)2=0,求(-2m2)-2m(5n-2m)+3n(6m-5n)-3n(4m-5n)的值.
- 【解析】试题分析:首先根据非负数之和为零则每一个非负数都是零求出m和n的值,将所求代数式根据多项式的乘法计算法则和合并同类项法则将多项式进行合并同类项,最后将m和n的值代入化简后的式子进行计算得出答案. 试题解析:由题意得2m-5=0,2m-5n+20=0, ∴m=,n=5,∴原式=2m2-4mn,当m=,n=5时,原式=. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:北师大版数学七年级下册 同步测试 1.3 同底数幂的除法 题型:单选题
当a>0时,下列关于幂的运算正确的是( )
A. a0=1 B. a﹣1=﹣a C. (﹣a)2=﹣a2 D. 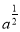 =
=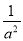
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下2.3.1 平行线的性质 同步练习 题型:单选题
如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )
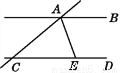
A. 40° B. 70° C. 80° D. 140°
B 【解析】试题解析:∵AB∥CD, ∴∠ACD+∠BAC=180°, ∵∠ACD=40°, ∴∠BAC=180°-40°=140°, ∵AE平分∠CAB, ∴∠BAE=∠BAC=×140°=70°, 故选B.查看答案和解析>>
科目:初中数学 来源:北师大版 七年级数学下册 第一章 整式的乘除 单项式与单项式相乘 专题练习题 含答案 题型:填空题
计算:-8x2y·(a-b)·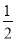 xy2·(
xy2·(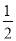 b-
b-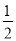 a)2=____________.
a)2=____________.
查看答案和解析>>
科目:初中数学 来源:北师大版 七年级数学下册 第一章 整式的乘除 单项式与单项式相乘 专题练习题 含答案 题型:单选题
某商场四月份售出某品牌衬衣b件,每件c元,营业额a元.五月份采取促销活动,售出该品牌衬衣3b件,每件打八折,则五月份该品牌衬衣的营业额比四月份增加( )
A.1.4a元 B.2.4a元 C.3.4a元 D.4.4a元
A 【解析】 试题分析:分别计算4、5月的营业额,相减得出结果. 【解析】 5月份营业额为3b×c=, 4月份营业额为bc=a, ∴a﹣a=1.4a. 故选A.查看答案和解析>>
科目:初中数学 来源:北师大版 七年级数学下册 第一章 整式的乘除 单项式与多项式相乘 专题练习题 含答案 题型:单选题
下列运算错误的是( )
A. -4a(2a2+3a-1)=-8a3-12a2+4a
B. am(am-a2+1)=a2m-am+2
C. (-3x2)·(4x2-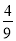 x+1)=-12x4+
x+1)=-12x4+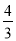 x3-3x2
x3-3x2
D. (2a2-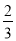 a-
a-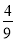 )·(-9a)=-18a3+6a2+4a
)·(-9a)=-18a3+6a2+4a
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册 第一章 整式的乘除 整式的运算 专题练习题 含答案 题型:解答题
已知一个长方形的长比它的宽的3倍少1厘米,如果把它的长减少2厘米,把它的宽增加2厘米,那么它的面积就增加6平方厘米,求原来长方形的面积.
24 【解析】试题分析:首先设原来长方形的宽为xcm,则它的长为(3x-1)cm,然后根据题意列出方程,从而求出x的值,然后求出原来长方形的面积. 试题解析:设原来长方形的宽为xcm,则它的长为(3x-1)cm, ∴(3x-3)(x+2)-x(3x-1)=6,解得x=3, 所以原来长方形的面积为3×(3×3-1)=24(cm2).查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:解答题
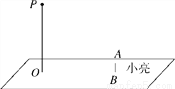
晚上,小亮在广场上乘凉.如图,线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯,小亮的身高为1.6m.
(1)在图中画出小亮在照明灯P照射下的影子BC;
(2)如果灯杆高PO=12m,小亮到灯杆的距离BO=13m,求小亮的影子BC的长度.
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年九年级(上)期末数学试卷 题型:单选题
已知在Rt△ABC中,∠C=90°,sinA=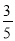 ,则tanB的值为( )
,则tanB的值为( )
A. 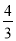 B.
B. 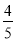 C.
C. 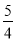 D.
D. 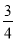
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com