
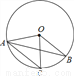
如图,点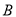 在⊙
在⊙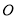 上,弦
上,弦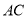 ∥
∥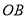 ,
, 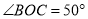 ,则
,则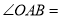 ( )
( )
A. 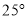 B.
B. 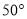 C.
C. 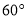 D.
D. 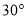
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源:上海市普陀区(五四制)2017-2018学年六年级上学期期末考试数学试卷 题型:单选题
六(1)班男生人数是女生人数的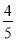 ,那么女生人数是全班人数的( )
,那么女生人数是全班人数的( )
A. 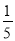 B.
B. 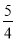 C.
C. 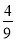 D.
D. 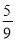
查看答案和解析>>
科目:初中数学 来源:山东省青岛市2017-2018学年上学期期末考试八年级数学试卷 题型:单选题
下列计算中,正确的是( )
A. 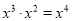 B.
B. 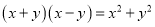
C. 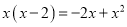 D.
D. 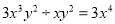
查看答案和解析>>
科目:初中数学 来源:新疆乌鲁木齐市2018届九年级上学期期末考试数学试卷 题型:填空题
如图,在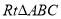 中,
中, 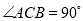 ,
, 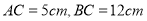 ,将
,将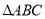 绕点
绕点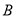 顺时针旋转
顺时针旋转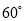 ,得到
,得到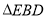 ,连接
,连接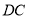 ,交
,交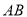 于点
于点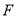 ,则
,则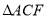 与
与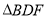 的周长之和为____
的周长之和为____  .
.
查看答案和解析>>
科目:初中数学 来源:新疆乌鲁木齐市2018届九年级上学期期末考试数学试卷 题型:单选题
某商场将进价为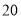 元∕件的玩具以
元∕件的玩具以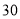 元∕件的价格出售时,每天可售出
元∕件的价格出售时,每天可售出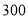 件,经调查当单价每涨
件,经调查当单价每涨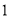 元时,每天少售出
元时,每天少售出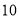 件.若商场想每天获得
件.若商场想每天获得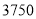 元利润,则每件玩具应涨多少元?若设每件玩具涨
元利润,则每件玩具应涨多少元?若设每件玩具涨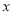 元,则下列说法错误的是( )
元,则下列说法错误的是( )
A. 涨价后每件玩具的售价是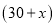 元
元
B. 涨价后每天少售出玩具的数量是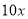 件
件
C. 涨价后每天销售玩具的数量是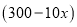 件
件
D. 可列方程为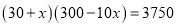
查看答案和解析>>
科目:初中数学 来源:河南省商丘市2017-2018学年上期七年级数学期末第一次模拟检测试卷 题型:解答题
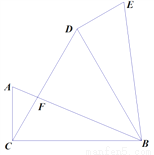
如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,求∠NEM的度数,并直接写出∠B′ME互余的角.
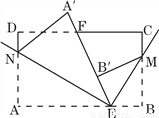
查看答案和解析>>
科目:初中数学 来源:河南省商丘市2017-2018学年上期七年级数学期末第一次模拟检测试卷 题型:单选题
已知O是直线AB上一点(点O在点A、B之间),OC是一条射线,则∠AOC与∠BOC的大小关系是( )
A. ∠AOC一定大于∠BOC B. ∠AOC一定小于∠BOC
C. ∠AOC一定等于∠BOC D. ∠AOC可能大于、等于或小于∠BOC
D 【解析】根据已知条件,画图如下: 由于OC是一条射线,其位置不固定,故∠AOC与∠BOC的关系也是不确定的. 故选:D.查看答案和解析>>
科目:初中数学 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:解答题
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
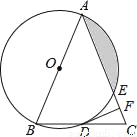
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
若单项式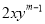 与
与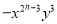 是同类项,则
是同类项,则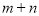 的值是_________.
的值是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com