
已知O是直线AB上一点(点O在点A、B之间),OC是一条射线,则∠AOC与∠BOC的大小关系是( )
A. ∠AOC一定大于∠BOC B. ∠AOC一定小于∠BOC
C. ∠AOC一定等于∠BOC D. ∠AOC可能大于、等于或小于∠BOC
D 【解析】根据已知条件,画图如下: 由于OC是一条射线,其位置不固定,故∠AOC与∠BOC的关系也是不确定的. 故选:D. 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源:贵州省黔南州2017-2018学年八年级上学期期末联考数学试卷 题型:填空题
若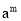 =2,
=2, 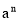 =3,则
=3,则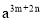 =
=
查看答案和解析>>
科目:初中数学 来源:新疆乌鲁木齐市2018届九年级上学期期末考试数学试卷 题型:解答题
如图,点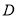 在⊙
在⊙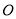 的直径
的直径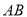 的延长线上,点
的延长线上,点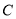 在⊙
在⊙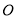 上,
上, 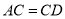 ,
, 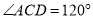 .
.
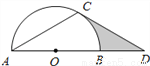
(1)求证: 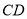 是⊙
是⊙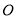 的切线;
的切线;
(2)若⊙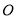 的半径为
的半径为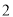 ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源:新疆乌鲁木齐市2018届九年级上学期期末考试数学试卷 题型:单选题
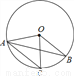
如图,点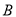 在⊙
在⊙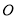 上,弦
上,弦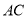 ∥
∥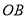 ,
, 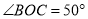 ,则
,则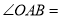 ( )
( )
A. 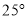 B.
B. 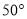 C.
C. 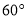 D.
D. 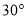
查看答案和解析>>
科目:初中数学 来源:河南省商丘市2017-2018学年上期七年级数学期末第一次模拟检测试卷 题型:解答题
如图,一副三角板的两个直角顶点重合在一起.
(1)若∠EON=110°,求∠MOF的度数;
(2)比较∠EOM与∠FON的大小,并写出理由;
(3)求∠EON+∠MOF的度数.
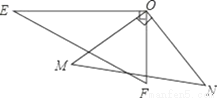
查看答案和解析>>
科目:初中数学 来源:河南省商丘市2017-2018学年上期七年级数学期末第一次模拟检测试卷 题型:单选题
下列4个图形中,能用∠1,∠AOB,∠O三种方法表示同一的图形是( )

A. A B. B C. C D. D
B 【解析】本题主要是对角的定义的考查. 当角的顶点处只有一个角时,可以用一个大写字母表示这个角,也可以用三个大写字母表示这个角. A、顶点O处有四个角,不能用∠O表示,错误; B、顶点O处有一个角,能同时用∠AOB,∠O,∠1表示,正确. C、顶点O处有三个角,不能用∠O表示,错误; D、∠1和∠O不表示同一角,错误; 故选B查看答案和解析>>
科目:初中数学 来源:河南省商丘市2017-2018学年上期七年级数学期末第一次模拟检测试卷 题型:填空题
如图,图中的角总共有____________个.
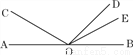
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:填空题
在平面直角坐标系中,将抛物线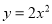 向上平移3个单位,得到的抛物线的函数表达式为 .
向上平移3个单位,得到的抛物线的函数表达式为 .
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
在△ABC中,AB=AC,点D为BC中点,DE⊥AB,DF⊥AC,垂足分别为E、F,求证:DE=DF
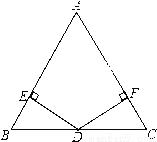
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com